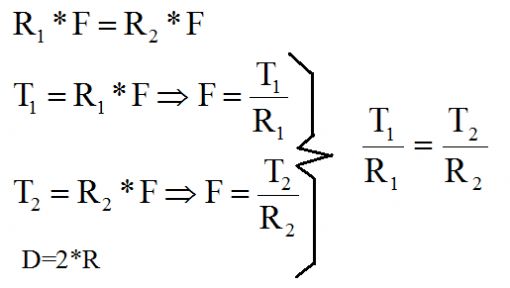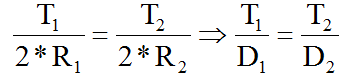- Katılım
- 13 Ocak 2007
- Mesajlar
- 2,298
- Puanları
- 1,866
- Yaş
- 47
TORK
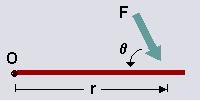
Torkun önce teknik tanımını yapalım: Tork bir nesneye etki eden kuvvetin o nesnenin ne kadar dönmesine yol açtığının ölçüsüdür. Nesne bir aks etrafında dönmektedir. Bu aksa biz pivot noktası (O), kuvvetin etki ettiği noktayla pivot noktası arasındaki mesafeye de Moment Kolu (r) diyoruz. Moment kolu aynı zamanda bir vektördür. Dolayısıyla tork, mesafe vektörüyle kuvvet vektörünün kesişme ürünüdür ve aralarındaki açının sinüsüyle orantılıdır., Formüle edersek: T = F x r = rF.Sin(Q). Tork Q açısının 90 derece olduğu noktada maksimumdur (sin = 1). Bu torkun teknik açıklaması.
Biraz da torku somutlaştırarak anlatmaya çalışalım; torkun ne olduğunu anlayabilmek için öncelikle kuvvetin ne olduğunu bilmemiz gerekir. Kuvvet, fizikte kabaca şöyle tanımlıdır: Hareket eden bir cismi durduran, duran bir cismi hareket ettiren, cisimlerin şekil, yön ve doğrultularını değiştiren etkiye Kuvvet denir.
Demek ki kuvvet ile hareket arasında doğrudan bir ilişki var. Nesnelerin eylemsizliği (momentumu) vardır, üzerlerine bir kuvvet etkimedikçe, pozisyonlarını korumaya eğimlidirler. Duruyorsa durmaya, hareket halindeyse harekete devam etme eğilimi her nesnenin doğasında gizlidir. Öyleyse örneğin duran bir masa dışardan bir kuvvet etki etmediği sürece kendiliğinden hareket etmeyecektir. Esasen masa nötr bir konumda değildir, üzerine etki eden kütle çekiminin etkisi altındadır. Buna rağmen yatay doğrultuda herhangi bir kuvvetin etkisi altında olmadığı için hareketsiz durmaktadır. Masaya bir de yatay doğrultuda bir kuvvet etkirse ve bu kuvvet masa ile zemin arasındaki sürtünme direncinden büyükse masamız hareket edecektir. Kısaca kuvvet bu; duran cisimleri hareket ettiren, hareket halinde olanları da duduran veya yavaşlatan etki... Dikkat ederseniz kuvvet tanımının içinde zaman ölçeği yok. Yani kuvvet tanımı bize hareketin zaman içindeki değişimini vermiyor. Bunu ileride daha ayrıntılı tartışacağız. Kaldığımız yere dönersek, kuvvet, büyüklüğü ve doğrultusu olan bir etki yani vektörel bir büyüklüktür. Kuvvet belli bir yön ve doğrultuda etkir. Bu yön doğrusal ise lineer bir kuvvetten, dairesel ise açısal/radyal bir kuvvetten söz ederiz çünkü kendi ekseni üzerinde hareket eden cisimlerin açısal momentumları vardır, söz konusu açısal momentumu değiştirecek olan şey de kuvvettir. Lineer vektörel kuvvete örnek yerçekimi, açısal/radyal vektörel kuvvete örnek olaraksa merkezkaç kuvveti verilebilir. Lineer vekötrel kuvvetin ölçüsü kg veya Newtondur. Yaklaşık 9,81 Newton 1 Kg kuvvete denk gelir. 1 kg ağırlığındaki bir cismi yerden kaldırmak için 1 kgın biraz üzerinde bir kuvvete ihtiyaç duyarız, aynı şekilde 1200 kg ağırlığındaki bir otomobili düz bir satıhta vites boştayken hareket ettirebilmemiz için yaklaşık 40-50 kg civarında bir lineer kuvvet uygulamamız gerekir. Yani bir nesneyi, iterken, çekerken ya da kaldırırken vektörü lineer bir kuvvete ihtiyaç duyarız.
Peki ya dairesel bir nesneyi kendi ekseni etrafında döndürmek istersek? İşte burda tork kavramı devreye girer...
Bir nesneyi kendi ekseni etrafında döndürmeye yarayan kuvvete tork ya da dönme momenti diyoruz. Tork, bir başka deyişle dönme momenti, Açısal Momentum kavramıyla iç içedir. Bir cismin çizgisel momentum vektörünün her hangi bir noktaya göre dönmesine açısal momentum denir. Cismin çizgisel momentum vektörü P,bu vektörü dönme noktasına bağlayan konum vektörü Y ise (Y ve P bir birine diktir), cismin açısal momentum vektörü J= Y x P olur. Açısal momentum zamana göre değişmiyor ve sabit kalıyorsa buna açısal momentumun korunumu denir (dJ/dt=sabittir). Sistemde açısal momentumun zamana göre değişimi aynı zamanda dönme momentini (tork) verir,Tork=dJ/dt.
Yukarıdaki bir başka akademik tanımdan anlaşılacağı üzere, torku bulabilmemiz için dönme eksenine dik etki eden kuvvet ile dönme eksenine olan mesafeyi çaRPMamız gerekir. Bunu aşağıdaki şekilde görebiliriz:
Bir kuvvet türü olarak torkun ölçüsü Newton-Metre ya da Kg-Metre cinsindendir (metrik sistemde). Bunu bir örnek vererek gösterelim: Çok büyük bir somun düşünün, bu somunu uzunluğu 1 metre olan bir anahtarla açmak istiyoruz. Anahtarın elimizdeki ucuna uyguladığımız kuvvet 20 kg olsun. Bu durumda somuna uygulanan tork 20 kgm (20 kg x 1 m) olacaktır. Anahtarın uzunluğunu 2 katına çıkarır ama kuvveti yarıya indirirsek (10 kg x 2 m ) yine 20 kgmlik bir tork elde ederiz. Ya da anahtar uzunluğunu ½ metreye düşürelim, aynı torku elde etmek için bu durumda anahtar ucuna uygulamamız gereken kuvvet 40 kg olacaktır (40 x ½ = 20 kgm). Görüldüğü üzere esasen bir manivela etkisinden söz ediyoruz. Yani tork dediğimiz şeyi sadece manivela kolunun uzunluğunu değiştirerek bile artırıp azaltabiliyoruz. Bu önemli çünkü transmisyon dediğimiz sistemin yaptığı tam da budur. Birinin üzerinde 40 diş bulanan bir dişli üzerinde 20 diş olan bir başka dişliyi çevirdiğinde de olan şey budur. 40 dişe sahip dişli 100 NM tork taşıyor olsun, dönme hızı da 100 RPM olsun, Bu durumda 20 dişe sahip dişli diğeri 1 tur döndüğünde 2 tur dönecek ama torku yarıya yani 50 NMye inecektir. Buradan çıkaracağımız sonuç, torkun dişliler ve/veya manivela kolu uzunluğu ile oynayarak artırılıp azaltılabileceğidir. Transmisyon birbirini döndüren farklı çaplarda bir dizi dişli grubundan oluşur ve görevi seçilen vitese göre torku artırıp azaltmaktır. Vites kutusu bir tür tork çarpanı işlevi görür. Vites kutuları forumda bir başka topik konusu edilebileceği için daha fazla üzerlerine yazmaya gerek duymuyorum.
Tork kısaca bu; bir mili kendi ekseni çevresinde döndüren kuvvet, bildiğiniz kuvvet yani. lineer kuvvetten tek farkı döndürme yönünün açısal olması ve bu nedenle eksen merkezi ile eksen çeperi arasındaki mesafenin (manivela/moment kolunun) hesaba dahil edilmesi zorunluluğu...
Bir vidayı sıkarken, bir civatayı sıkar veya gevşetirken uyguladığımız kuvvet torkun ta kendisidir. En yalın tork tanımı da budur.
Motorlar da tork üretirler. Piston üzerine basınç uygulayan genleşme gazları bu basıncı biyel kolu aracılığı ile pistondan krank mili jurnaline iletir. Jurnal ile krank aksı arasındaki mesafe moment koludur. Baştaki açıklamaları hatırlarsak motorda nasıl tork üretildiğini de idrak etmiş olacağız. Motor torku anlık tork ve averaj tork olarak ikiye ayrılır. Kataloglarda verilen tork averaj torktur. Motorda üretilen tork şanzıman ve diferansiyelden geçerek tekerleklere iletilir. Bu esnada şanzıman ve diferansiyeldeki dişli oranları mertebesinde katlanır, yani artar. Bununla ilgili detaylı bilgi TORK VE RPM İLİŞKİSİ başlığı altında verilmiştir.
İŞ
İş yukarıda da görmüştük, esasen hareket yani nesnenin yer değiştirmesi olarak değerlendirilebilir. Bir İŞin olabilmesi için
1. yer değiştirme miktarına,
2. yer değiştirmede harcanan kuvvete ihtiyacımız vardır.
Bu da w = f x d formülüyle ifade edilir. İş yapabilmek için kuvvet harcamak yetmez, yer değiştirme zorunlu şarttır. Örneğin bir vidayı 10 kgm torkla sıkalım, vida bir noktada iyice sıkıştıktan sonra dönmesini durduracaktır. Bu noktada biz hala aynı kuvveti uygulamaya devam etsek bile, vida artık dönmeyeceği için iş yapmış sayılmayız. Başka bir örnek: Herhangi bir duvarı 50 kg kuvvetle itelim, ne olur? Hiç bir şey olmaz, yaptığımız iş kuvvet harcadığımız halde 0dır. Ama aynı 50 kglık kuvveti bir arabayı itmekte kullanırsak ve arabayı mesela 20 m itersek, iş yapmış oluruz ve yaptığımız işin miktarı 50 kg x 20 m = 100 kgm olur. İŞ kavramını niçin anlatıyoruz? Çünkü beygir gücü iş yapma hızıdır, beygir gücünü anlatırken, İŞ kavramına ihtiyaımız olacak. Bir elektirik motoru tork üretir, çalışır durumda bir elektirk motorunun milini sabitlenmiş bir mengenede sıkıştırırsak elektrik motoru mil dönmediği halde tork üretmeye devam eder ama mil dönmediği için üretilen tork mesela 200 NM olsa bile yapılan iş 0dır. Bunu da bir yere not edelim.
BEYGİR GÜCÜ
Torku öğrendik, beygirgücü ne o halde? Beygirgücünü öğrenmeden önce fizikteki güç kavramına bir açıklık getirmemiz gerekiyor. Türkçemiz günlük kullanımda güç ve kuvvet arasında pek bir ayrım gözetmiyor ama fizikte bu iki terim farklı kavramları karşılamak üzere kullanılıyor. Kalan kısımda da bu ayrıma özenle dikkat edeceğiz. Kuvveti yukarıda girişte tanımladık, tork da bir kuvvet türüydü, bunu gördük. Güç için de tanımlar muhtelif. En bilinen tanımlardan başlayalım isterseniz:
Güç aşağıdakilerin hepsidir:
1. Birim zamanda üretilen veya harcanan enerji miktarı yani enerji dönüşüm hızıdır.
2. Birim zamanda yapaılan İŞ miktarı yani İŞ yapma hızıdır.
3. Kuvvetin yineleme oranı ya da hızıdır (hangi hızda kuvvet ürretiyorsunuz).
4. Kinetik enerjideki değişim oranı/hızıdır.
Gücün ölçüsü metrik sistemde jul/saniye, bir başka deyişle Wattdır. Genel formulü P = F x d /T ya da W/Tdir. Burada P: güç, F: kuvvet, d: mesafe, T: zaman ve W: iştir. Enerji taşıyan ve bu enerjiyi kullanan herşeyin gücü vardır; bir ampulün, bir matkabın, bir insanın, bir arabanın, bir atın...
Bu gücü Watt cinsinden ölçebileceğimiz gibi başka birimlerle de ölçebiliriz. Beygirgücü mesela motorların gücünü ölçme birimidir ve kolayca Watt cinsine çevrilebilir. Beygirgücü yukarıda tanımlanan güç ile aynı şeydir, sadece spesifik bir alandaki kullanımına işaret eder.
Beygirgücü kavramını İngiliz mucit James Watt ortaya attı. İcat ettiği buhar makinesini kömür madenlerine satmak isterken, makinenin gücünü, o dönemde İngiliz madenlerinde yaygın olarak kullanılan pony cinsi atların gücüyle karşılaştırmak istedi. Böyle yaparak maden sahiplerini ikna etmek istiyordu ancak kullandığı değişkenler keyfidir ve gerçekten bir atın gücünü tam olarak ölçüp ölçmediği belirsizdir.
Watt, madenlerde yaptığı gözlemlerde, bir atın, 12 feet (3,66 m) uzunluğunda bir çıkrık koluna bağlı 180 lblik ( 82 kg) bir kömür kovasını dakikada 2,4 kez (144/saat) dönerek maden ocağından çıkardığını fark etti. Yukarıda verdiğimiz güç formülüne bu değerleri koyarsak P = W/T veya F x d /t olduğuna göre P = 180 x 2,4 x 2 pi x 12) 1 dakika = 32,572 lbf/dakika sonucu buldu. Bunu 33.000 lbfa yuvarladı. Bu da 550 lbf/saniye yapar. Bunun metrik sistemdeki karşılığı 75 m/s ya da 735 W civarıdır. Kısacası 75 kglık bir ağırlığı 1 saniyede 1 metre yukarı kaldıran güce 1 beygir gücü diyoruz. Bir motorun beygir gücü genellikle hesaplanır çünkü nihayetinde beygir gücü soyut matematiksel bir kavramdır, bir ekstrapolasyondur. Beygir gücü yaygın olarak, ölçülen torktan hesaplanır. Bunun imoeriyal formülü de şudur: HP = Tork x RPM /5252. Paydadaki sayı 550 lb-ft/s değerinin radyan cinsinden ifade edilmesinin bir sonucu olarak formülde yer almaktadır. Unutmayın, formül imperyaldir, NM cinsinden tork kullanabilmek için metrik sisteme çevrilmesi gerekir. Su tipi dinamometreler beygir gücünü hesaplamayıp doğrudan ölçerler. Ölçüm yöntemi su sıcaklığındaki artışın ölçülmesine dayanır (enerji salınım hızı). Beygir gücü başka pek çok yöntemle de hesaplanabilir. Ama bu hesapların tamamına yakını teoriktir, pratikten hesaplama için yukarıdaki formül kullanılır. Aşağıda bazı tipik teorik beygir gücü hesaplama yöntemleri verilmiştir:
HP = Süpap lifti /500 x Hacim (imperyal)
HP = ((Hız/234)^3) x Ağırlık (imperyal)
HP = BMEP x Hacim x RPM /792 (imperyal)
HP = Jul / saniye / 0,735 (akselerasyondan hesaplama)
HP = TE x yakıt Akışı (PPH) x 7473
Özetler ve begirgücünü herkesin anlayabileceği bir perspektife koymak istersek; beygirgücü için motor torkunun yineleme hızıdır diyebiliriz. Yani motor ne sıklıkta tork üretiyor, bunu beygirgücü ile ölçüyoruz. Bu nedenle tork ölçümünde zaman komponenti yok ama beygirgücü ölçümünde zaman komponenti vardır. Beygirgücü motorun zamana karşı yaptığı işin ölçüsüdür. Birim zamanda motorumuz ne kadar iş yapmış bunu zamanla ölçüyoruz.
Peki iş ne? İş yer değiştirmedir. Enerjiyi kuvvete dönüştürerek bir nesnenin yerini değiştirebiliriz yani onu hareket ettiririz. Yer değiştirme için bir kuvvet harcamamız ve bir mesafe katetmemiz gerekir. İş bu ikisinin çarpımıdır (kuvvet x yol). Yol 0ken yani hareket etmiyorken, kuvvet harcasak bile iş yapmış olmayız; kuvvet X, yol 0 ise 0X = 0 olur. İşi anladık; motorumuz ne iş yapar?.. Aracı A noktasından B noktasına götürür. A noktasından B noktasına kuvvet (tork) kullanarak götürür. Peki ne kadar zamanda götürür? Onu da beygirgücü ile ölçeriz ve bu yüzden bir aracın SON HIZInın diğer değişkenleri sabit varsayarsak tek ölçüsü beygir gücüdür.
RPM
RPM dakikada dönüş hızı ya da miktarının İngilizcedeki karşılığı. Fizikteki karşılığı alınan mesafedir (yol). Bir mil yol alır mı? Evet, üzerine işaretlediğimiz bir nokta 1 turda 2pi radyan kadar yol almaktadır. Milin çapı 1 santim ise ve mesela dakikada 1000 devir yapıyorsa alınan yol 1 x 2 x 3,14 x 1000 = 6,28 metre olacaktır. RPM böylece bize 1 dakikada alınan yolu vermektedir.
TORK VE RPM İLİŞKİSİ
Tork ve RPM bir madalyonun 2 yüzü gibidirler. Biri olmadan diğeri anlamsızdır. RPM olmadan tork hiç bir işe yaramayan bir rakamdan ibarettir. Tork ve RPM aynı büyüklüğün farklı yansımalarından başka şey değildirler. Tork ve RPM transmisyon aracılığı ile birbiriyle değiştirilebilir yani istediğimiz miktarda torku RPMe veya tersine çevirebiliriz. Bunu bize transmisyon sağlar. Örneğin yarıçapı 1 metre olan bir makara düşünün, bu makaraya 6280 metre halat sarılı. Makaramız 100 kgm gücünde ve dakikada 1000 RPM devre sahip bir motor tarafından döndürülüyor olsun. Makarayı 6280 m yukarıya çıkaralım ve ucuna 100 kglık bir ağırlık bağlayalım. Motorumuz 100 kgm torka ve 1000 RPMe sahip olduğu için bu 100 kglık ağırlığı 1 dakikada 6280 metre yukarıya çıkaracaktır. Motorumuzun beygir gücü (100 x 1000 /728) 137 HPdir. Evet 100 kgm torka ve 1000 RPMe sahip bir motorla 100 kglık ağırlığı 1 dakikada 6280 m yukarıya çıkardık ama bu kadar beklemek istemiyoruz, şu işi ½ dakikada halledelim diyoruz. Bu durumda yine 100 kgm torka ama 2000 RPM devre sahip bir motor monte ediyoruz makaramıza. Şimdi yine 100 kglık bir ağırlığı 6280 m yukarıya çıkarıyoruz ama sadece yarım dakikada. Tork değişmedi, RPM iki katına çıktı, süremiz yarıya indi. Bu motorun beygir gücü de 100 x 2000 / 728 = 274 HP. Yani ilk motorun iki katı. Tork değişmediği halde beygir gücünü iki katına çıkardığımızda alınan süreyi yarıya indiriyoruz, buraya DİKKAT (!). Peki makaraya 50 kgm torka ve 4000 RPM devre sahip bir motor bağlarsak ne olur? Ağırlık 100 kg > 50 kgm tork olduğu için motorumuz bu ağırlığı kaldıramayacaktır. Elimizde ne var? Bize yetmeyen 50 kgm tork ve ihtiyacımızın 2 katı RPM var. İhtiyaç fazlası bu RPMi ihtiyacımız olan torka çeviremez miyiz? Evet, bunu makara ile motor mili arasına hızı yarıya düşüren (2:1) bir çevre uzunluğuna sahip bir dişli seti ile yapabiliriz. Bu durumda RPM 2000e düşer, tork 100 kgmye çıkar beygir gücü değişmez ( 50 x 4000 /728 = 274 HP). Gördüğünüz gibi beygir güçleri aynı, tork ve RPMleri farklı 2 motordan 50 kgm torka sahip olanı ağırlığı doğrudan kaldıramadı ama araya 2:1 oranlı bir transmisyon koyduğumuzda 2 motor yalnızca beygirgücü açısından değil her açıdan eşitlendi. İşte transmisyon, torka ihtiyacımız olduğunda fazla RPMi torka, RPMe ihtiyacımız olduğunda da fazla torku RPMe çevirir. Tork ve RPM birbirine dönüşebilen fiziksel büyüklüklerdir. Madalyonumuz beygir gücüdür, bu madalyonun bir yüzü tork, diğer yüzü RPMdir. Bu nedenle, 8000 RPMde 50 NM tork üreten bir motorla 2000 RPMde 200 NM tork üreten bir motoru 4:1lik basit bir transmisyon kolayca eşitler. Daha fazla RPMe neden ihtiyaç duyarsınız? Daha hızlı gitmek için; Daha fazla torka neden ihtiyaç duyarsınız? Daha fazla yük taşımak/çekmek için... Transmisyon size ne istiyorsanız onu verir: Daha fazla RPM veya daha fazla tork.
AKSELERASYON/DESELERASYON (HIZLANMA/YAVAŞLAMA)
Birim zamanda hızdaki değişimdir. Hızdaki artış bizi daha çok ilgilendirdiği için akselerasyona kabaca hızdaki artış diyebiliriz. Türkçedeki karşılığı ivme veya ivmelenmedir. Hızdaki artış sabit olabileceği gibi değişken de olabilir. Biz hızdaki artışla yani hızlanmayla ilgiliyiz. Hızlanma belirli bir zaman periyodunda hız kazanmadır, hız artışıdır. Birim zamanda mesela X hızından 2X hızına çıkmaktır. Newtonun ikinci yasası bize Akselerasyonun formülünü verir: A (akselerasyon) = F (kuvvet) / M (kütle).
TORK AKSELERASYON İLİŞKİSİ
Evet, artık onca laftan sonra meselenin özüne geldik: Bir otomobili hızlandıran tork mudur, beygir gücü müdür? Soruyu yanıtlamadan önce tork ve beygir gücünün birbirinin alternatifi, birbirini ikame eden kavramlar olmadığını bir kez daha hatırlatalım. Unutmayın, tork ürettiğiniz her an otomatikman beygir gücü de üretirsiniz. Beygir gücü torkun bir niceliğidir.
Newtonun ikinci yasası der ki, bir cisim üzerindeki net kuvvet, cismin kütlesi ile ivmesinin çarpımına eşittir. Bunu formule edersek F = Mx A ile gösterebilir, buradan da A = F/Mi elde ederiz. Yani kuvvetin cismin kütlesine bölümü bize ivmeyi (hızlanmayı) verir. Öyleyse bir arabayı hızlandıran şey, arabanın kütlesi değişmediğine göre, ona etki eden kuvvettir kuvvetteki artıştır. Yukarıda görmüştük arabamızın motoru da bir kuvvet üretir ve buna tork demiştik,.
Demek ki, arabayı hızlandıran şey motorun torkudur. ..
Öyle midir?
Evet diyenler yanıldı, arabayı hızlandıran kuvvet motor torku değil, arabanın tahrik tekerlerinin tabanında oluşan kuvvettir ve bu iki kuvvet (motor torku ile teker kuvveti) sadece 1. Viteste paraleldir. hiç bir durumda ise aynı değildir. Teker tabanında oluşan itme kuvveti lineerdir ve Newton cinsinden ifade edilir. Motor torku ise açısaldır ve NewtonMetre ile ifade edilir. Bu iki kuvvet arasında bir ilişki vardır. Teker tabanındaki kuvvetin kaynağı motor torkudur ama kendisi değildir. İkisi son kertede farklı şeylerdir. Bunu aşağıda örnekleriyle göreceğiz. Motor şaftını doğrudan tekere bağlasaydık bu iki kuvvet tümüyle paralel olacaktı, ne var ki araya torku ve RPMi istediğimiz gibi artırıp azaltan bir mekanizma, transmisyonu koyduğumuz için bu iki kuvvet arasındaki ilişki karmaşıklaşır. Yukarıdaki Newton formülüne ( A = F/M) motor torkunu yerleştiremezsiniz çünkü tork NM cinsindendir, oysa formüldeki F Newton cinsinden olmak zorundadır. Örnek vermek gerekirse 1200 kg ağırlığındaki bir aracın 1 Glik ivme ile hızlanabilmesi için kuvvet ne olmalıdır? F = MAdan 1200 x 9,81 = 11,772 Newton. Peki bu arabanın maksimum torku 1750 RPMde 240 NM olsun. Teker tabanında oluşan 11,772 Nluk kuvveti 240 NMlik motor torku ile nasıl ilişkilendireceğiz? Formüle doğrudan motor torkunu koyamadık çünkü birimler farklı. Gördüğünüz üzere A = F/M formülü motor torku için işlemiyor. Öyleyse motor torku ile tekerlek tabanındaki kuvveti nasıl ilişkilendireceğiz? Onu da BEYGİR GÜCÜ AKSELERASYON İLİŞKİSİ başlığı altında inceleyeceğiz.
BEYGİR GÜCÜ AKSELERASYON İLİŞKİSİ
Akselerasyonu açıklarken Newtonun ikinci yasasına atıfta bulunmuştuk. Yine bu yasaya göre, herhangi bir akselerasyondan söz edebilmemiz için kuvvet nesneye sıfırdan farklı bir zaman diliminde nesneyle AYNI HIZDA uygulanmalıdır. Açarsak, akselerasyonun şartı;
1. Kuvvet nesneye nesnenin sahip olduğu hızda uygulanacak, nesneyle aynı hızda uygulanacak,
2. Kuvvetin uygulama süresi 0dan farklı olacak.
Peki, güç tanımını hatırlayalım: belli bir hızda ve belli bir zaman zarfında uygulanan kuvvet. Bu tanım ile akselerasyonun şartları aynı. Demek ki, bir nesne üzerine uygulanan akslerasyon kuvveti o hızda uygulanan güç tarafından belirleniyor ! Bunu arabaya uygularsak aşağıdaki sonuçlara ulaşırız:
Akstaki Beygir Gücü = Dönüş Hızı x Tork
Lastik Tabanındaki Beygir Gücü = Kuvvet x Hız - buradan:
Akselerasyon Kuvveti (Fa) = Güç ( P) / Hız (V).
Yani Akselerasyon = Güç / Hız.
Nereden nereye geldik... Durmayalım, devam edelim:
Güç = Kuvvet x Hız ise (bu aynı zamanda beygi gücü tanımımızdır) ve Kuvvet = Kütle x Akselerasyon ise Güç = Kütle x Akselerasyon x Hız olur. Buradan:
Akselerasyon = Güç / Kütle x Hız denklemini elde ederiz. Momentum = Kütle x Hız olduğuna göre formülümüzü Akselerasyon = Güç / Momentum olarak sadeleştirebiliriz.
Newtonun ikinci yasası bizi A = F/Mden A = P / V ye, oradan da A = P / M e getirdi. Bu formülden görüleceği üzere akselerasyon ve hız ters orantılı. Hız arttıkça akselerasyon azalıyor, güç arttıkça akselerasyon artıyor.
Beygir gücünün akselerasyon ile ilişkisi açık. F = MA formülü uyarınca maksimum akselerasyon daima maksimum tork noktasında gelir ama bu tork motor torku değildir, tekerlek aksı torkudur. Tekerlek aksında tork maksimum olduğunda motorda tork maksimumda olmayabilir çünkü araya transmisyon girmiştir. İşte bu nedenle tekerlekteki maksimum kuvveti belirlerken motor torkuna değil, beygirgücüne bakacağız,..
Tüm bu açıklamalardan çıkan sonuç, akselerasyon söz konusu olduğunda belirleyici olan kuvvetin motor torku değil, tekerlek tabanında oluşan kuvvet olduğudur. Çünkü arabayı zemin üzerinde ileriye iten kuvvet budur, motor torku değil. Bu kuvvet transmisyon yüzünden motor torkundan farklıdır. Transmisyon motor torkuyla tekerlek taban kuvveti arasındaki doğrudan ilişkiyi kırar ve onu dolaylı hale getirir. Bunu aşağıdaki örneklerde göreceğiz. Sonuç olarak bizim için esas olan tekerlek taban kuvvetidir ve Tekerlek tabanındaki bu kuvvet iki yöntemle hesaplanabilir:
1. Tork yöntemi:
Tekerlek Taban Kuvveti (N) = (Tork (NM) x Şanzıman Oranı x Diferansiyel oranı) / Lastik yarıçapı (m)
2. Beygir Gücü Yöntemi:
Tekerlek Taban Kuvveti (N) = 820,275 x (Güç (HP) / Hız (Kms)
Hangi yöntemle hesaplarsanız hesaplayın, tekerlek taban kuvveti olarak aynı sonucu elde edersiniz.
Araya transmisyon girdiğinde motordaki tork tekerlek tabanına nasıl yansır bunu geçerli bir örnekle görelim:
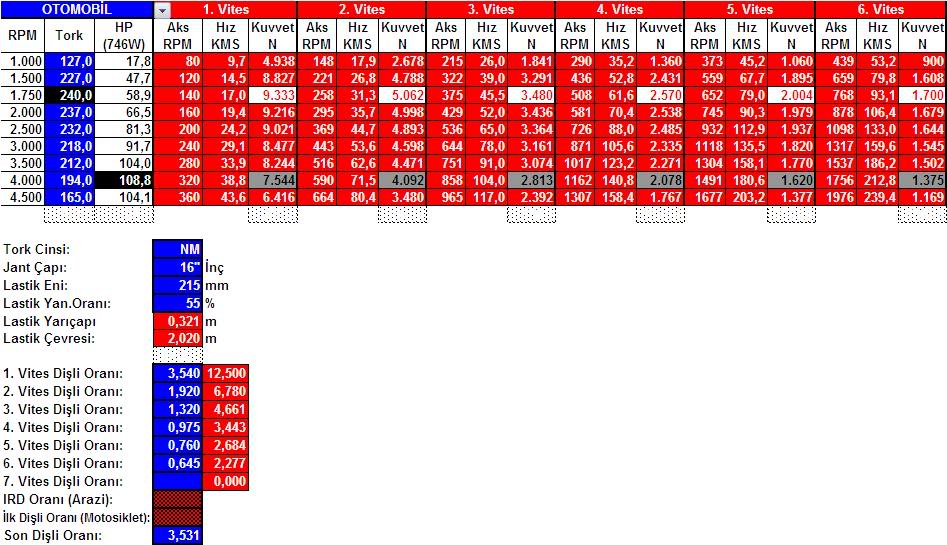
Tabloda verili değerler 2007 Citroen C4 1.6 hdI Picasso modeline aittir. Tablodan görüleceği üzere motor torku herhangi bir devirde sabit olduğu halde tekerlek tabanındaki kuvvet seçilen vitese bağlı olarak değişmektedir. Tablodaki örnekte 240 NM maksimum motor torku 1.750 RPMde geliyor. Motor 1.750 RPMdeyken 1. Vites ile 6. Vites arasında 9.333 Newtondan 2.004 Newtona kadar teker tabanındaki kuvvet değişiklik arz ediyor, oysa motorun torku değişmiyor, o maksimumda ama teker tabaındaki kuvvet seçilen vitese bağlı olarak sürekli değişiyor. Tekerlek tabanındaki kuvvetle motor torkunun örtüştüğü tek bir yer var: 1. vites. Aracın maksimum hızlanması 1. viteste gerçekten motorun maksimum torkuna paraleldir. Ne var ki , vites değiştirdiğinizde işin rengi değişiyor, 1. viteste varolan bu ilişki kırılıyor. Örneğin 2. viteste motor 1.750 RPMdeyken tekerlek tabanındaki kuvvet 5.062 N ve ikinci vites içindeki en yüksek taban kuvveti bu devirde geliyor. Ama aynı yol hızında vitesi 1e alırsak 8.400 Newtondan 6.400 Newtona azalan bir taban kuvveti elde ediyoruz. Diyelim ki 3. viteste maksimum tork devrinde (motor 1.750 RPMdeyken) seyahat ediyorsunuz. Bu durumda yol hızınız 45,5 kms, tekerlek devriniz 375 RPM olur. Şimdi hızlanmaya karar verdiniz. Bir de baktınız motor 1750 RPMde yani maksimum torkunu verdiği devirde. Şöyle düşünüyorsunuz: Madem ki A = F/M, o halde en yüksek hızlanmayı şimdi elde ederim . Yanlış!.. O esnada gaza basarsanız, elde edeceğiniz maksimum taban kuvveti 3.480N ama bir alt vitese yani ikinci vitese geçerseniz yol hızınıza eşit motor devri 2.543 RPM ve o RPMdeki motor torkunuz 232 NMnin altında ama 2. vites 375 RPMde tekerlek tabanındaki kuvvet tam 4.800 N (!)
Evet, aracın maksimum hızlanacağını düşündüğünüz anda teker tabanında 3.480 N kuvvet vardı ama bir alt vitese geçtiniz ve 3.480Ndan 4.800 Na çıktınız. Hani motor maksimum torkunu verdiği devirde aracımız da maksimum hızlanmaya sahip oluyordu?.. Yok öyle bir şey!
Konuyu bu noktadan irdelemeye devam edelim...
Aşağıda ağırlıkları ve diğer özellikleri birbirinin aynı 3 motora ait grafikler göreceksiniz. Bu üç motoru kırmızı, yeşil be mavi motor olarak adlandıralım. BU 3 motoru da birbirinin tıpatıp aynı 3 ayrı otomobile monte edelim ve neler oluyor bir göz atalım:
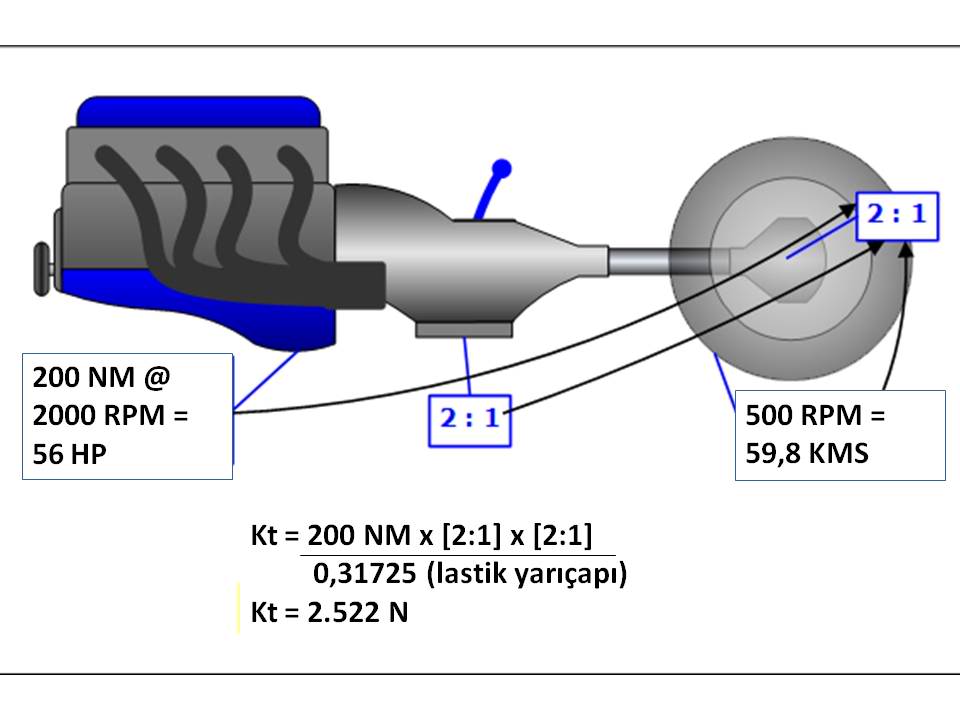
Yukarıdaki illüstrasyondan görüleceği üzere ilk motorumuz Mavi motor. 2000 RPMde 200 NM torka sahip ve 56 HP gücünde. 2:1 oranlı bir vites kutusuna bağlı. Bu vites kutusu da yine 2:1 oranlı bir diferansiyele bağlı. Diferansiyel aksları 195/65R15 ebatlarında bir tekerleği döndürüyor. Motorumuz 200 NM tork verdiği 2000 RPMde çalışırken vites kutusu bunu 2:1 oranla 1000 RPMe düşürüyor, vites kutusundan sonra gelen diferansiyel de devri 1.000 RPMden 500 RPMe düşürüyor. 500 RPMde dönen bir 195/65R15 tekerlek dakikada 997 metre yani saatte 59,8 km hızla yol alıyor. Özetle; 1.000 kg ağırlığındaki otomobilimiz Mavi motorla donatılmış ve saatte 59,8 km hızla yol alıyor. Bu hızdayken tekerlek tabaındaki kuvvet 2522 Newton. Yani aracımız Mavi motorla 2000 RPMdeyken 59,8 kms hızla yol alıyor. Bu hızda motorun torku 200 NM, beygir gücü 56 HP, lastik tabanındaki kuvvet ise 2.522 Newton. Şimdi de ikinci illüstrasyona bakalım:
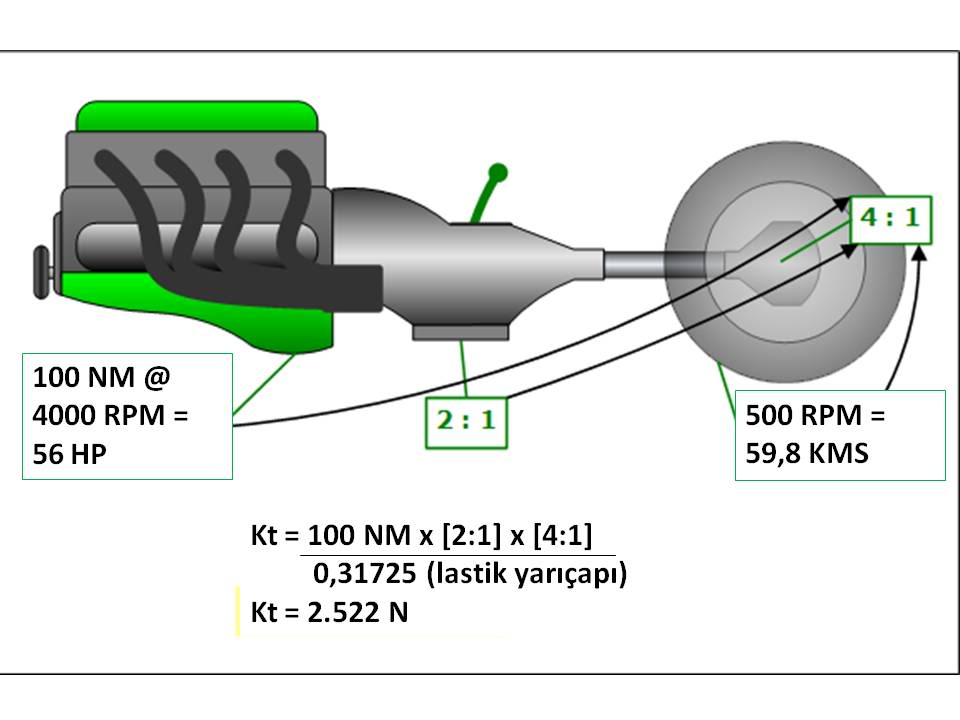
Otomobilimiz aynı ama motorumuz bu defa Yeşil motor ve şu özelliklere sahip: 4.000 devirde 100 NM tork üretiyor. Bu devirde beygir gücü yine 56 HP. Diğer otomobilden tek farkı aynı yol hızında gidebilmek için 2:1 yerine 4:1 oranlı bir diferansiyele sahip. Bu sayede otomobilimiz yine aynı hızda, 59,8 kms ile yol alabiliyor. Peki bu durumda tekerlek tabanında oluşan kuvvet ne? Yine aynı, 2.522 Newton. Şimdi de 3. İllüstrasyona bakalım:
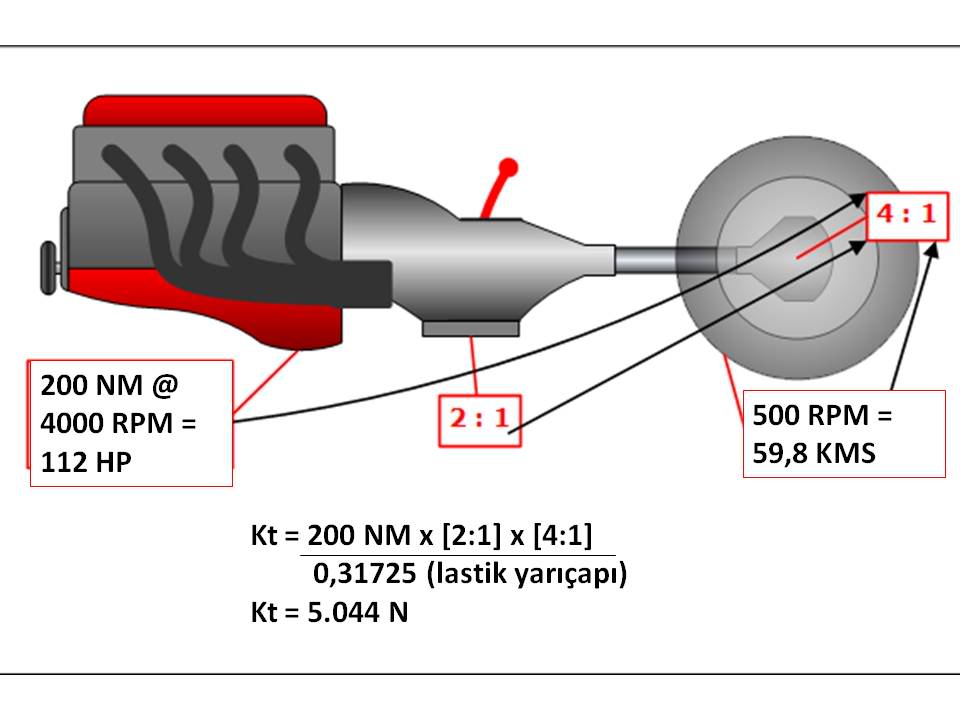
Kırmızı motorla donatılmış otomobilimiz de aynı hızla yol alıyor: 59,8 kms. Bu hıza ulaşmak için otomobilimiz yeşil motorlu otomobildekiyle aynı 4:1 oranlı diferansiyel kullanıyor çünkü Kırmızı motor 4000 RPMde 200 NM tork üretirken beygir gücü de diğer iki motorun iki katı yani 112 HP güce sahip. Peki bu otomobilin tekerlek tabaında oluşan kuvvet ne? Tam 5.044 Newton, diğer iki otomobilin 2 katı!. Şimdi senaryo şu:
Birbirinin aynı 3 otomobil var, ağırlıkları (1.000 kg) ve tekerlekleri aynı, sadece motorları farklı. Her biri bu 3 motorla donatılmış durumda ve yolda 59,8 kms hızla yan yana yol alıyorlar. Peki aynı anda dibine kadar gaza bassalar hangisi daha çabuk hızlanır?
1. 2.000 RPMde 200 NM tork üreten Mavi motorlu otomobil mi? (56 HP)
2. 4.000 RPMde 100 NM tork üreten Yeşil motorlu otomobil mi? (56 HP)
3. 4.000 RPMde 200 NM tork üreten Kırmızı motorlu otomobil mi? (112 HP)
Bunu anlamak için bakacağımız yer gördüğünüz gibi motorun torku değil çünkü Mavi motorla Kırmızı motorun torkları aynı. Peki nereye bakacağız? Elbette ki, tekerlek tabanında oluşan kuvvete:
1. Mavi motorlu otomobil: 2.522 N A = F / M = 2522/1000 = 2,522 m/s
2. Yeşil motorlu otomobil: 2.522 N A = F / M = 2522/1000 = 2,522 m/s
3. Kırmızı motorlu otomobil: 5.044 N A = F / M = 5044/1000 = 5,044 m/s
Demek ki, ~60 kms hızda giderken en yüksek akselerasyon değerine Kırmızı motorlu otomobil sahip olacak. Kırmızı otomobil aynı zamanda diğerleri arasında en yüksek beygir gücüne (56/56/112 HP) sahip olan otomobil!...
Bu sonuç hiç şaşırtıcı değil. Yukarıda bir yerlerde motor torkuyla tahrik tekerleri arasındaki ilişkiyi transmisyon kırıyor demiştik. Nasıl kırdığını işte gördünüz. Bu olguyu CVT şanzımanlı bir otomobilde daha iyi anlarız çünkü CVT şanzıman tork ve RPM arasındaki ilişkiyi her devirde bire bir tutturan bir şanzıman türüdür, en ideal şanzıman türüdür. Bir de CVT şanzımanlı bir araca bakalım:
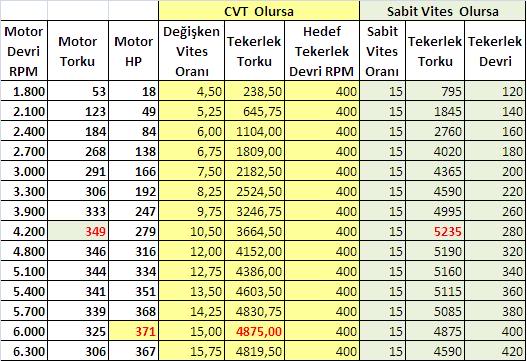
Yukarıdaki tablodan görüleceği üzere CVT şanzımanda sabit bir hızda en yüksek hızlanma maksimum beygir gücünün oluştuğu noktada geliyor: 6.000 RPM 371 HP ve 4.875 N.
Ama sabit bir viteste, aynı vites içinde kalma kaydıyla ve hız sabit değilken en yüksek taban kuvveti maksimum torkun oluştuğu 4.200 RPMde 349 NMde geliyor: 5.235 N. BU durum gerçek hayatta sadece 1. vites hızlanmalarına tekebul ediyor, onun dışında her viteste sabit bir hızdayken maksimum hızlanma bir alt viteste genellikle maksimum beygir gücünün oluştuğu devirde veya o civarda geliyor.
Öyleyse ne zaman vites değiştireceğiz? Klasik CVT şanzımanlı bir araçta vites sürekli değiştiği için, maksimum teker kuvveti daima maksimum HP devrinde gelir, bunu yukarıda gördük. Ama bizim araçlarımız CVT şanzımanlı değil. Öyleyse ne zaman vites değiştirelim maksimum hızlanma için?
Elbette asla maksimum tork devrinde değil ama isterseniz bunu ayrı bir konu başlığı olarak ele alalım çünkü mevcut konu mini bir kitap yazacak kadar uzadı.
Onun yerine beygir gücü ile ilgili hesaplamalara devam edelim:
Şöyle bir senaryo oluşturalım: 200 LBF ( 272 Nm) torku 3.000 devirde (114 HP) ve 5.000 devirde (190 HP) üreten iki otomobil 0-160 parkurunda yarışırsa ne olur? Olacak olan şu: 1. otomobil yarışın hemen başında öne geçer, neden? Çünkü 2. otomobil daha az tork üretirken, ilk otomobil 200 LBF torku ondan önce 2.000 devirde üretir. Ama daha sonra 1. otomobilnın deviri arttıkça ürettiği tork azalacak, o vitesteki son hıza ulaşacak ve dişli oranları yüzünden daha az tork üreteceği (ve daha yavaş hızlanacağı) 2. vitese geçmek zorunda kalacak. Oysa 2. otomobil çok yüksek devirlere kadar 1. viteste kalabilir. Böylece 1. otomobil 3. vitese geçtiğinde 2. otomobil 2. vitese yeni geçmiş olacaktır ve sonuçta yarışı 2. otomobil kazanır. Burdan çıkan sonuç ne? Her iki otomobilin torkları aynı olduğu halde yarışı beygir gücü fazla olanın kazanacağıdır. Birinin beygir gücü fazladır çünkü aynı torka rağmen %66 daha fazla RPMe sahiptir. İşte bu fazla RPM ihtiyaç (hızlanma) anında torka çevrilir. Unutmayın, yüksek RPM ve yüksek tork yüksek beygir gücü demektir.
Şimdi de bir başka örnek: 1.000 kg ağırlığında bir otomobili 0 KMS hızdan (0 m/s) hızdan 100 KMS (27,78 m/s) hıza 10 saniyede çıkarmak ve aynı arabayı yine 10 saniyede 100 KMS hızdan hızdan 200 KMS (55,56 m/s) hıza çıkarmak ne kadar kuvvet gerektirir?
Her iki durumda da a=(27,78-0)/10=2,778 ve a=(55,56-27,78)/10=2,778. Yani ivme 2,778 m/s^2 (veya 0,35 G) )
f=m*a olduğuna göre f=1.000*2,778=2.778 N. Yani arabayı ister 0dan 100 km/s hıza, ister 100den 200 km/s hıza çıkartın, daima aynı miktarda KUVVETE yani torka ihtiyacınız var.
Ama 2.778 N kuvveti 0 m/s hızda ve 55,56 m/s aynı kuvveti kullanmak aynı sonucu doğurmuyor. İsterseniz gerekli gücü d = d1 + V1.t + (½).a.t^2 ve P= E/T formüllerini kullanarak bulalım:
x=0+0*10+0,5*2,778*10^2=138,9 m yani 0 m/s hızdan 27,78 m/s hıza 10 saniyede ulaşana kadar otomobilin katettiği mesafe. Peki diğeri ne? x=0+27,78*10+0,5*2,778*10^2=694,5 m bu da 27,78 m/s hızdan 55,56 m/s hıza ulaşana kadar katettiği mesafe.
İş formulü W = F x D olduğuna göre W=1.000*138,9=138.900 Jul ve P=138900/10=13.890 Watt (18,6 HP) W=1.000*694,5=694.500 Jul ve P=694.500/10=69.450 Watt (93,0 HP)
Sonuçta görüldüğü üzere iki otomobili de eşit miktarda hızlandırmak için aynı miktarda kuvvet yani tork gerekiyor ama daha hızlı olan arabayı hızlandırmak için tam 5 katı fazla beygir gücü gerekiyor. a = p/mv denklemine göre hızı ne kadar artırırsak, hızlanma o kadar azalıyor, Bu durumda gücü aynı oranda artırmak gerek hızlanmayı sabit tutmak için.
Özetlersek, vites değiştirmediğiniz zaman aynı viteste kalarak yapılan hızlanmada, aracınızın hızlanma grafiği, motorunuzun tork grafiğinin bir izdüşümüdür ve böyle bir hızlanmada aracınızın tork grafiğinin altında kalan alanın büyüklüğü bize hızlanmadaki başarımızı verir.
Ama ya vites değiştiriyorsak, ki değiştiriyoruz; o zaman ne olur? O zaman aracımızın hızlanma grafiği tork eğrisini değil HP eğrisini izler.
Yine bu topik veya bir başka topik altında beygir gücü grafiklerini nasıl okumalıyız meselesini de tartışmaya açmak istiyorum. Beygir gücü grafiklerini iyi okuyarak spesifik bir otomobille ilgili çok şey öğrenebiliriz. Bunun için güç bandı kavramını iyi anlamamız gerekiyor. Her motorun bir güç bandı vardır. Bu güç bandı temelde ikiye ayrılır:
1. Toplam Güç Bandı: rölanti devrinden, redline devirne kadar tüm devirleri kapsayan güç bandıdır.
2. Operasyonel Güç Bandı: Bırakın yarışları, günlük kullanımda dahi 1. vites haricinde hemen hiç kullanılmayan ilk 1500-2000 rpm dışarda bırakılarak hesaplanan güç bandı.
Bu iki güç bandına bakarak motorla ilgili şu değerleri elde edebiliriz:
a. Maksimum HPnin %80inin devir badının % kaçında yer aldığını görebilir ve diğer araçlarla kıyaslayabiliriz.
b. İster toplam güç bandı isterse operasyonel güç bandı içindeki ortalama HPyi hesaplarız. BU değer maksimum HPden daha önemlidir.
c. Güç bandını rölanti-redline arası belirleyebileceğimiz gibi, mesala redline/2 redline arası sınırlı tutabiliriz (eğer yarışıyorsak redline/2nin altı çok önemli değildir).
Yani beygir gücün grafiğini yukarıdaki örnekte olduğu gibi çeşitli yöntemlerle anlamlandırabiliriz. Dilerseniz bunu da bir başka topik altında ele alalım.
SONUÇ
Beygir gücü bize torkun hızını verir. Hızlı tork, yani yüksek devirde yüksek tork hedeftir, idealdir, Yüksek devirde yüksek tork, yüksek beygir gücü demektir. Düşük devirde yüksek tork ise düşük devirde yüksek beygir gücü demektir. Açalım...
1000 RPMde 200 LBF tork veren motor, 2000 RPMde 100 LBF tork veren motordan farksızdır. Çünkü ikisi de devri 1500 RPMe düşüren/çıkaran bir transmisyonla ( 1,5:1/0,75:1) eşitlenir. Tork her iki motor için 1500 RPMde eşitlenir: 133 LBF. Neden? Çünkü bu iki motor beygir gücü açısından eşittir: 38 HP. Dikkat ederseniz hem 1000, hem 1500 hem de 2000 RPMde HP aynıdır, değişmez çünkü bu iki motorun torkları farklıdır ama RPMleri onları hem kuvvet hem de HP açısından eşitler.
Tork yüksek devirde gelirse, yüksek HP elde ederiz. Yüksek devirde gelen tork bize daha fazla hız için kuvvetten ya da daha fazla kuvvet için hızdan fedakarlık yapma imkanı tanır ama düşük devirde gelen tork bize bu imkanı tanımaz. 10 RPMde 20.000 LBF veren bir motor devasa bir torka sahiptir ve 0-10 RPM arasında müthiş bir hızlanma sağlar ama aracımız bu müthiş hızlanma zarfında topu topu 20 metre yol alır çünkü bu devirdeki beygir gücü sadece 38 HPdir! HIZ OLMADAN HIZLANMA BİR HİÇTİR. Bize hızı veren şey ise RPMdir, tek başına tork değil. RPM ve tork birarada bize beygir gücünü verir. Bizim her halukarda bilmemiz gereken yegane şey beygir gücüdür, tork değil. 2000 RPMde 200 LBF tork veren bir motor 2000 RPMde 100 LBF tork veren bir motordan aynı devirde iki kat fazla beygir gücüne sahiptir (38 HPye karşı 76 HP) ama aynı motor 4000 RPMde 100 LBF tork veren motorla aynıdır çünkü 2:1lik bir transmisyon bu iki motoru hemen eşitler. Oysa beygir güçleri değişmez: 76 HP. Transmisyon dişli oranlarıyla artıp azaltılabildiği için torku bilmemize gerek yoktur, torku biliyorsak transmisyon dişli oranlarını da bilmemiz gerekir, aksi halde bildiğimiz tork değerleri bir işe yaramaz. Arabamız sadece motordan ibaret değildir, şanzımanı, diferansiyeli ve tekerlekleri de vardır, bunlar da hesaba katıldığında motor torkunun tekbaşına bir anlamı kalmaz. Oysa beygir güxünü biliyorsak ne şanzıman ne de diferansiyel dişli oranlarıyla uğraşmamıza gerek kalmaz. Zaten beygir gücü dediğimiz şey belirli bir torkun hangi devirde geldiğinden başka bir şey değildir.
Arabalar söz konusu olduğunda bilmemiz gereken tek büyüklük BEYGİR GÜCÜDÜR, torku unutun.
Ve evet, son olarak şu meşhur mottoya gelelim: HP araba sattırır, tork yarış kazandırır. Bu durum motor torku söz konusu olduğunda doğru değil, bunu gördük. Doğrusu ne?
Doğrusu şu:
Maksimum HP araba sattırır, ortalama HP yarış kazandırır.
SÖZÜN ÖZÜ:
TORK VE RPM TRANSMİSYON (MANİVELA) ARACILIĞI İLE BİRBİRLERİNE DÖNÜŞTÜRÜLEBİLEN FİZİKSEL BÜYÜKLÜKLERDİR. HIZ İÇİN RPME, HIZLANMA VE YÜK ÇEKME/TAŞIMA İÇİN TORKA İHTİYAÇ DUYARIZ. İHTİYAÇ DUYDUĞUMUZDA ELİMİZDEKİ FAZLA RPMİ TORKA, FAZLA TORKU DA RPME ÇEVİRİRİZ. ÖRNEĞİN RPMİ YARIYA DÜŞÜREREK TORKU İKİ KATINA YA DA TORKU YARIYA DÜŞÜREREK RPMİ İKİ KATINA ÇIKARIRIZ. BEYGİR GÜCÜ ELİMİZDEKİ RPMİN NE KADARINI TORKA YA DA ELİMİZDEKİ TORKUN NE KADARINI RPME ÇEVİREBİLECEĞİMİZİ GÖSTEREN HESAPLANABİLİR BİR NİCELİKTİR. DOLAYISIYLA İÇİNDE HEM TORKU HEM DE RPMİ BARINDIRIR. NE KADAR FAZLA BEYGİR GÜCÜMÜZ VARSA RPM/TORK DÖNÜŞÜMÜNDE O KADAR ÇOK ESNEKLİĞİE KAVUŞURUZ. BU NEDENLE MOTORUMUZLA İLGİLİ BİLMEMİZ GEREKEN TEK FİZİKSEL NİCELİK BEYGİR GÜCÜDÜR. BUNU BİLİYORSAK, DİĞERLERİNİ BİLMEYE GEREK YOKTUR.
ALINTIDIR
Torkun önce teknik tanımını yapalım: Tork bir nesneye etki eden kuvvetin o nesnenin ne kadar dönmesine yol açtığının ölçüsüdür. Nesne bir aks etrafında dönmektedir. Bu aksa biz pivot noktası (O), kuvvetin etki ettiği noktayla pivot noktası arasındaki mesafeye de Moment Kolu (r) diyoruz. Moment kolu aynı zamanda bir vektördür. Dolayısıyla tork, mesafe vektörüyle kuvvet vektörünün kesişme ürünüdür ve aralarındaki açının sinüsüyle orantılıdır., Formüle edersek: T = F x r = rF.Sin(Q). Tork Q açısının 90 derece olduğu noktada maksimumdur (sin = 1). Bu torkun teknik açıklaması.

Biraz da torku somutlaştırarak anlatmaya çalışalım; torkun ne olduğunu anlayabilmek için öncelikle kuvvetin ne olduğunu bilmemiz gerekir. Kuvvet, fizikte kabaca şöyle tanımlıdır: Hareket eden bir cismi durduran, duran bir cismi hareket ettiren, cisimlerin şekil, yön ve doğrultularını değiştiren etkiye Kuvvet denir.
Demek ki kuvvet ile hareket arasında doğrudan bir ilişki var. Nesnelerin eylemsizliği (momentumu) vardır, üzerlerine bir kuvvet etkimedikçe, pozisyonlarını korumaya eğimlidirler. Duruyorsa durmaya, hareket halindeyse harekete devam etme eğilimi her nesnenin doğasında gizlidir. Öyleyse örneğin duran bir masa dışardan bir kuvvet etki etmediği sürece kendiliğinden hareket etmeyecektir. Esasen masa nötr bir konumda değildir, üzerine etki eden kütle çekiminin etkisi altındadır. Buna rağmen yatay doğrultuda herhangi bir kuvvetin etkisi altında olmadığı için hareketsiz durmaktadır. Masaya bir de yatay doğrultuda bir kuvvet etkirse ve bu kuvvet masa ile zemin arasındaki sürtünme direncinden büyükse masamız hareket edecektir. Kısaca kuvvet bu; duran cisimleri hareket ettiren, hareket halinde olanları da duduran veya yavaşlatan etki... Dikkat ederseniz kuvvet tanımının içinde zaman ölçeği yok. Yani kuvvet tanımı bize hareketin zaman içindeki değişimini vermiyor. Bunu ileride daha ayrıntılı tartışacağız. Kaldığımız yere dönersek, kuvvet, büyüklüğü ve doğrultusu olan bir etki yani vektörel bir büyüklüktür. Kuvvet belli bir yön ve doğrultuda etkir. Bu yön doğrusal ise lineer bir kuvvetten, dairesel ise açısal/radyal bir kuvvetten söz ederiz çünkü kendi ekseni üzerinde hareket eden cisimlerin açısal momentumları vardır, söz konusu açısal momentumu değiştirecek olan şey de kuvvettir. Lineer vektörel kuvvete örnek yerçekimi, açısal/radyal vektörel kuvvete örnek olaraksa merkezkaç kuvveti verilebilir. Lineer vekötrel kuvvetin ölçüsü kg veya Newtondur. Yaklaşık 9,81 Newton 1 Kg kuvvete denk gelir. 1 kg ağırlığındaki bir cismi yerden kaldırmak için 1 kgın biraz üzerinde bir kuvvete ihtiyaç duyarız, aynı şekilde 1200 kg ağırlığındaki bir otomobili düz bir satıhta vites boştayken hareket ettirebilmemiz için yaklaşık 40-50 kg civarında bir lineer kuvvet uygulamamız gerekir. Yani bir nesneyi, iterken, çekerken ya da kaldırırken vektörü lineer bir kuvvete ihtiyaç duyarız.
Peki ya dairesel bir nesneyi kendi ekseni etrafında döndürmek istersek? İşte burda tork kavramı devreye girer...
Bir nesneyi kendi ekseni etrafında döndürmeye yarayan kuvvete tork ya da dönme momenti diyoruz. Tork, bir başka deyişle dönme momenti, Açısal Momentum kavramıyla iç içedir. Bir cismin çizgisel momentum vektörünün her hangi bir noktaya göre dönmesine açısal momentum denir. Cismin çizgisel momentum vektörü P,bu vektörü dönme noktasına bağlayan konum vektörü Y ise (Y ve P bir birine diktir), cismin açısal momentum vektörü J= Y x P olur. Açısal momentum zamana göre değişmiyor ve sabit kalıyorsa buna açısal momentumun korunumu denir (dJ/dt=sabittir). Sistemde açısal momentumun zamana göre değişimi aynı zamanda dönme momentini (tork) verir,Tork=dJ/dt.
Yukarıdaki bir başka akademik tanımdan anlaşılacağı üzere, torku bulabilmemiz için dönme eksenine dik etki eden kuvvet ile dönme eksenine olan mesafeyi çaRPMamız gerekir. Bunu aşağıdaki şekilde görebiliriz:

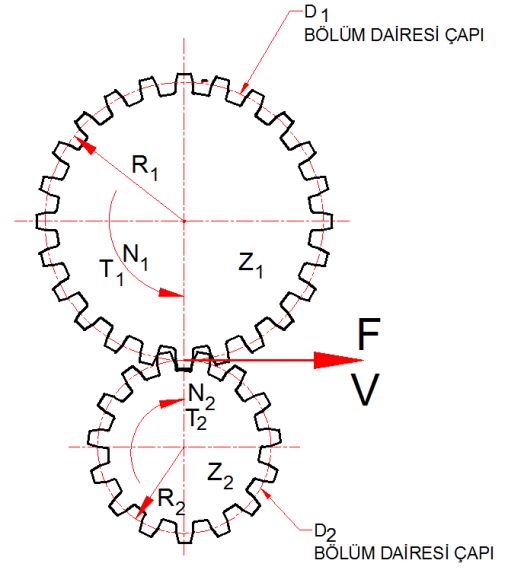
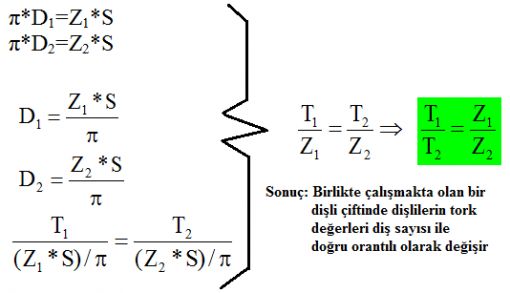
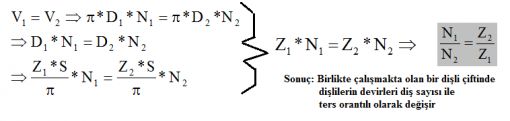
Bir kuvvet türü olarak torkun ölçüsü Newton-Metre ya da Kg-Metre cinsindendir (metrik sistemde). Bunu bir örnek vererek gösterelim: Çok büyük bir somun düşünün, bu somunu uzunluğu 1 metre olan bir anahtarla açmak istiyoruz. Anahtarın elimizdeki ucuna uyguladığımız kuvvet 20 kg olsun. Bu durumda somuna uygulanan tork 20 kgm (20 kg x 1 m) olacaktır. Anahtarın uzunluğunu 2 katına çıkarır ama kuvveti yarıya indirirsek (10 kg x 2 m ) yine 20 kgmlik bir tork elde ederiz. Ya da anahtar uzunluğunu ½ metreye düşürelim, aynı torku elde etmek için bu durumda anahtar ucuna uygulamamız gereken kuvvet 40 kg olacaktır (40 x ½ = 20 kgm). Görüldüğü üzere esasen bir manivela etkisinden söz ediyoruz. Yani tork dediğimiz şeyi sadece manivela kolunun uzunluğunu değiştirerek bile artırıp azaltabiliyoruz. Bu önemli çünkü transmisyon dediğimiz sistemin yaptığı tam da budur. Birinin üzerinde 40 diş bulanan bir dişli üzerinde 20 diş olan bir başka dişliyi çevirdiğinde de olan şey budur. 40 dişe sahip dişli 100 NM tork taşıyor olsun, dönme hızı da 100 RPM olsun, Bu durumda 20 dişe sahip dişli diğeri 1 tur döndüğünde 2 tur dönecek ama torku yarıya yani 50 NMye inecektir. Buradan çıkaracağımız sonuç, torkun dişliler ve/veya manivela kolu uzunluğu ile oynayarak artırılıp azaltılabileceğidir. Transmisyon birbirini döndüren farklı çaplarda bir dizi dişli grubundan oluşur ve görevi seçilen vitese göre torku artırıp azaltmaktır. Vites kutusu bir tür tork çarpanı işlevi görür. Vites kutuları forumda bir başka topik konusu edilebileceği için daha fazla üzerlerine yazmaya gerek duymuyorum.
Tork kısaca bu; bir mili kendi ekseni çevresinde döndüren kuvvet, bildiğiniz kuvvet yani. lineer kuvvetten tek farkı döndürme yönünün açısal olması ve bu nedenle eksen merkezi ile eksen çeperi arasındaki mesafenin (manivela/moment kolunun) hesaba dahil edilmesi zorunluluğu...
Bir vidayı sıkarken, bir civatayı sıkar veya gevşetirken uyguladığımız kuvvet torkun ta kendisidir. En yalın tork tanımı da budur.
Motorlar da tork üretirler. Piston üzerine basınç uygulayan genleşme gazları bu basıncı biyel kolu aracılığı ile pistondan krank mili jurnaline iletir. Jurnal ile krank aksı arasındaki mesafe moment koludur. Baştaki açıklamaları hatırlarsak motorda nasıl tork üretildiğini de idrak etmiş olacağız. Motor torku anlık tork ve averaj tork olarak ikiye ayrılır. Kataloglarda verilen tork averaj torktur. Motorda üretilen tork şanzıman ve diferansiyelden geçerek tekerleklere iletilir. Bu esnada şanzıman ve diferansiyeldeki dişli oranları mertebesinde katlanır, yani artar. Bununla ilgili detaylı bilgi TORK VE RPM İLİŞKİSİ başlığı altında verilmiştir.
İŞ
İş yukarıda da görmüştük, esasen hareket yani nesnenin yer değiştirmesi olarak değerlendirilebilir. Bir İŞin olabilmesi için
1. yer değiştirme miktarına,
2. yer değiştirmede harcanan kuvvete ihtiyacımız vardır.
Bu da w = f x d formülüyle ifade edilir. İş yapabilmek için kuvvet harcamak yetmez, yer değiştirme zorunlu şarttır. Örneğin bir vidayı 10 kgm torkla sıkalım, vida bir noktada iyice sıkıştıktan sonra dönmesini durduracaktır. Bu noktada biz hala aynı kuvveti uygulamaya devam etsek bile, vida artık dönmeyeceği için iş yapmış sayılmayız. Başka bir örnek: Herhangi bir duvarı 50 kg kuvvetle itelim, ne olur? Hiç bir şey olmaz, yaptığımız iş kuvvet harcadığımız halde 0dır. Ama aynı 50 kglık kuvveti bir arabayı itmekte kullanırsak ve arabayı mesela 20 m itersek, iş yapmış oluruz ve yaptığımız işin miktarı 50 kg x 20 m = 100 kgm olur. İŞ kavramını niçin anlatıyoruz? Çünkü beygir gücü iş yapma hızıdır, beygir gücünü anlatırken, İŞ kavramına ihtiyaımız olacak. Bir elektirik motoru tork üretir, çalışır durumda bir elektirk motorunun milini sabitlenmiş bir mengenede sıkıştırırsak elektrik motoru mil dönmediği halde tork üretmeye devam eder ama mil dönmediği için üretilen tork mesela 200 NM olsa bile yapılan iş 0dır. Bunu da bir yere not edelim.
BEYGİR GÜCÜ
Torku öğrendik, beygirgücü ne o halde? Beygirgücünü öğrenmeden önce fizikteki güç kavramına bir açıklık getirmemiz gerekiyor. Türkçemiz günlük kullanımda güç ve kuvvet arasında pek bir ayrım gözetmiyor ama fizikte bu iki terim farklı kavramları karşılamak üzere kullanılıyor. Kalan kısımda da bu ayrıma özenle dikkat edeceğiz. Kuvveti yukarıda girişte tanımladık, tork da bir kuvvet türüydü, bunu gördük. Güç için de tanımlar muhtelif. En bilinen tanımlardan başlayalım isterseniz:
Güç aşağıdakilerin hepsidir:
1. Birim zamanda üretilen veya harcanan enerji miktarı yani enerji dönüşüm hızıdır.
2. Birim zamanda yapaılan İŞ miktarı yani İŞ yapma hızıdır.
3. Kuvvetin yineleme oranı ya da hızıdır (hangi hızda kuvvet ürretiyorsunuz).
4. Kinetik enerjideki değişim oranı/hızıdır.
Gücün ölçüsü metrik sistemde jul/saniye, bir başka deyişle Wattdır. Genel formulü P = F x d /T ya da W/Tdir. Burada P: güç, F: kuvvet, d: mesafe, T: zaman ve W: iştir. Enerji taşıyan ve bu enerjiyi kullanan herşeyin gücü vardır; bir ampulün, bir matkabın, bir insanın, bir arabanın, bir atın...
Bu gücü Watt cinsinden ölçebileceğimiz gibi başka birimlerle de ölçebiliriz. Beygirgücü mesela motorların gücünü ölçme birimidir ve kolayca Watt cinsine çevrilebilir. Beygirgücü yukarıda tanımlanan güç ile aynı şeydir, sadece spesifik bir alandaki kullanımına işaret eder.
Beygirgücü kavramını İngiliz mucit James Watt ortaya attı. İcat ettiği buhar makinesini kömür madenlerine satmak isterken, makinenin gücünü, o dönemde İngiliz madenlerinde yaygın olarak kullanılan pony cinsi atların gücüyle karşılaştırmak istedi. Böyle yaparak maden sahiplerini ikna etmek istiyordu ancak kullandığı değişkenler keyfidir ve gerçekten bir atın gücünü tam olarak ölçüp ölçmediği belirsizdir.
Watt, madenlerde yaptığı gözlemlerde, bir atın, 12 feet (3,66 m) uzunluğunda bir çıkrık koluna bağlı 180 lblik ( 82 kg) bir kömür kovasını dakikada 2,4 kez (144/saat) dönerek maden ocağından çıkardığını fark etti. Yukarıda verdiğimiz güç formülüne bu değerleri koyarsak P = W/T veya F x d /t olduğuna göre P = 180 x 2,4 x 2 pi x 12) 1 dakika = 32,572 lbf/dakika sonucu buldu. Bunu 33.000 lbfa yuvarladı. Bu da 550 lbf/saniye yapar. Bunun metrik sistemdeki karşılığı 75 m/s ya da 735 W civarıdır. Kısacası 75 kglık bir ağırlığı 1 saniyede 1 metre yukarı kaldıran güce 1 beygir gücü diyoruz. Bir motorun beygir gücü genellikle hesaplanır çünkü nihayetinde beygir gücü soyut matematiksel bir kavramdır, bir ekstrapolasyondur. Beygir gücü yaygın olarak, ölçülen torktan hesaplanır. Bunun imoeriyal formülü de şudur: HP = Tork x RPM /5252. Paydadaki sayı 550 lb-ft/s değerinin radyan cinsinden ifade edilmesinin bir sonucu olarak formülde yer almaktadır. Unutmayın, formül imperyaldir, NM cinsinden tork kullanabilmek için metrik sisteme çevrilmesi gerekir. Su tipi dinamometreler beygir gücünü hesaplamayıp doğrudan ölçerler. Ölçüm yöntemi su sıcaklığındaki artışın ölçülmesine dayanır (enerji salınım hızı). Beygir gücü başka pek çok yöntemle de hesaplanabilir. Ama bu hesapların tamamına yakını teoriktir, pratikten hesaplama için yukarıdaki formül kullanılır. Aşağıda bazı tipik teorik beygir gücü hesaplama yöntemleri verilmiştir:
HP = Süpap lifti /500 x Hacim (imperyal)
HP = ((Hız/234)^3) x Ağırlık (imperyal)
HP = BMEP x Hacim x RPM /792 (imperyal)
HP = Jul / saniye / 0,735 (akselerasyondan hesaplama)
HP = TE x yakıt Akışı (PPH) x 7473
Özetler ve begirgücünü herkesin anlayabileceği bir perspektife koymak istersek; beygirgücü için motor torkunun yineleme hızıdır diyebiliriz. Yani motor ne sıklıkta tork üretiyor, bunu beygirgücü ile ölçüyoruz. Bu nedenle tork ölçümünde zaman komponenti yok ama beygirgücü ölçümünde zaman komponenti vardır. Beygirgücü motorun zamana karşı yaptığı işin ölçüsüdür. Birim zamanda motorumuz ne kadar iş yapmış bunu zamanla ölçüyoruz.
Peki iş ne? İş yer değiştirmedir. Enerjiyi kuvvete dönüştürerek bir nesnenin yerini değiştirebiliriz yani onu hareket ettiririz. Yer değiştirme için bir kuvvet harcamamız ve bir mesafe katetmemiz gerekir. İş bu ikisinin çarpımıdır (kuvvet x yol). Yol 0ken yani hareket etmiyorken, kuvvet harcasak bile iş yapmış olmayız; kuvvet X, yol 0 ise 0X = 0 olur. İşi anladık; motorumuz ne iş yapar?.. Aracı A noktasından B noktasına götürür. A noktasından B noktasına kuvvet (tork) kullanarak götürür. Peki ne kadar zamanda götürür? Onu da beygirgücü ile ölçeriz ve bu yüzden bir aracın SON HIZInın diğer değişkenleri sabit varsayarsak tek ölçüsü beygir gücüdür.
RPM
RPM dakikada dönüş hızı ya da miktarının İngilizcedeki karşılığı. Fizikteki karşılığı alınan mesafedir (yol). Bir mil yol alır mı? Evet, üzerine işaretlediğimiz bir nokta 1 turda 2pi radyan kadar yol almaktadır. Milin çapı 1 santim ise ve mesela dakikada 1000 devir yapıyorsa alınan yol 1 x 2 x 3,14 x 1000 = 6,28 metre olacaktır. RPM böylece bize 1 dakikada alınan yolu vermektedir.
TORK VE RPM İLİŞKİSİ
Tork ve RPM bir madalyonun 2 yüzü gibidirler. Biri olmadan diğeri anlamsızdır. RPM olmadan tork hiç bir işe yaramayan bir rakamdan ibarettir. Tork ve RPM aynı büyüklüğün farklı yansımalarından başka şey değildirler. Tork ve RPM transmisyon aracılığı ile birbiriyle değiştirilebilir yani istediğimiz miktarda torku RPMe veya tersine çevirebiliriz. Bunu bize transmisyon sağlar. Örneğin yarıçapı 1 metre olan bir makara düşünün, bu makaraya 6280 metre halat sarılı. Makaramız 100 kgm gücünde ve dakikada 1000 RPM devre sahip bir motor tarafından döndürülüyor olsun. Makarayı 6280 m yukarıya çıkaralım ve ucuna 100 kglık bir ağırlık bağlayalım. Motorumuz 100 kgm torka ve 1000 RPMe sahip olduğu için bu 100 kglık ağırlığı 1 dakikada 6280 metre yukarıya çıkaracaktır. Motorumuzun beygir gücü (100 x 1000 /728) 137 HPdir. Evet 100 kgm torka ve 1000 RPMe sahip bir motorla 100 kglık ağırlığı 1 dakikada 6280 m yukarıya çıkardık ama bu kadar beklemek istemiyoruz, şu işi ½ dakikada halledelim diyoruz. Bu durumda yine 100 kgm torka ama 2000 RPM devre sahip bir motor monte ediyoruz makaramıza. Şimdi yine 100 kglık bir ağırlığı 6280 m yukarıya çıkarıyoruz ama sadece yarım dakikada. Tork değişmedi, RPM iki katına çıktı, süremiz yarıya indi. Bu motorun beygir gücü de 100 x 2000 / 728 = 274 HP. Yani ilk motorun iki katı. Tork değişmediği halde beygir gücünü iki katına çıkardığımızda alınan süreyi yarıya indiriyoruz, buraya DİKKAT (!). Peki makaraya 50 kgm torka ve 4000 RPM devre sahip bir motor bağlarsak ne olur? Ağırlık 100 kg > 50 kgm tork olduğu için motorumuz bu ağırlığı kaldıramayacaktır. Elimizde ne var? Bize yetmeyen 50 kgm tork ve ihtiyacımızın 2 katı RPM var. İhtiyaç fazlası bu RPMi ihtiyacımız olan torka çeviremez miyiz? Evet, bunu makara ile motor mili arasına hızı yarıya düşüren (2:1) bir çevre uzunluğuna sahip bir dişli seti ile yapabiliriz. Bu durumda RPM 2000e düşer, tork 100 kgmye çıkar beygir gücü değişmez ( 50 x 4000 /728 = 274 HP). Gördüğünüz gibi beygir güçleri aynı, tork ve RPMleri farklı 2 motordan 50 kgm torka sahip olanı ağırlığı doğrudan kaldıramadı ama araya 2:1 oranlı bir transmisyon koyduğumuzda 2 motor yalnızca beygirgücü açısından değil her açıdan eşitlendi. İşte transmisyon, torka ihtiyacımız olduğunda fazla RPMi torka, RPMe ihtiyacımız olduğunda da fazla torku RPMe çevirir. Tork ve RPM birbirine dönüşebilen fiziksel büyüklüklerdir. Madalyonumuz beygir gücüdür, bu madalyonun bir yüzü tork, diğer yüzü RPMdir. Bu nedenle, 8000 RPMde 50 NM tork üreten bir motorla 2000 RPMde 200 NM tork üreten bir motoru 4:1lik basit bir transmisyon kolayca eşitler. Daha fazla RPMe neden ihtiyaç duyarsınız? Daha hızlı gitmek için; Daha fazla torka neden ihtiyaç duyarsınız? Daha fazla yük taşımak/çekmek için... Transmisyon size ne istiyorsanız onu verir: Daha fazla RPM veya daha fazla tork.
AKSELERASYON/DESELERASYON (HIZLANMA/YAVAŞLAMA)
Birim zamanda hızdaki değişimdir. Hızdaki artış bizi daha çok ilgilendirdiği için akselerasyona kabaca hızdaki artış diyebiliriz. Türkçedeki karşılığı ivme veya ivmelenmedir. Hızdaki artış sabit olabileceği gibi değişken de olabilir. Biz hızdaki artışla yani hızlanmayla ilgiliyiz. Hızlanma belirli bir zaman periyodunda hız kazanmadır, hız artışıdır. Birim zamanda mesela X hızından 2X hızına çıkmaktır. Newtonun ikinci yasası bize Akselerasyonun formülünü verir: A (akselerasyon) = F (kuvvet) / M (kütle).
TORK AKSELERASYON İLİŞKİSİ
Evet, artık onca laftan sonra meselenin özüne geldik: Bir otomobili hızlandıran tork mudur, beygir gücü müdür? Soruyu yanıtlamadan önce tork ve beygir gücünün birbirinin alternatifi, birbirini ikame eden kavramlar olmadığını bir kez daha hatırlatalım. Unutmayın, tork ürettiğiniz her an otomatikman beygir gücü de üretirsiniz. Beygir gücü torkun bir niceliğidir.
Newtonun ikinci yasası der ki, bir cisim üzerindeki net kuvvet, cismin kütlesi ile ivmesinin çarpımına eşittir. Bunu formule edersek F = Mx A ile gösterebilir, buradan da A = F/Mi elde ederiz. Yani kuvvetin cismin kütlesine bölümü bize ivmeyi (hızlanmayı) verir. Öyleyse bir arabayı hızlandıran şey, arabanın kütlesi değişmediğine göre, ona etki eden kuvvettir kuvvetteki artıştır. Yukarıda görmüştük arabamızın motoru da bir kuvvet üretir ve buna tork demiştik,.
Demek ki, arabayı hızlandıran şey motorun torkudur. ..
Öyle midir?
Evet diyenler yanıldı, arabayı hızlandıran kuvvet motor torku değil, arabanın tahrik tekerlerinin tabanında oluşan kuvvettir ve bu iki kuvvet (motor torku ile teker kuvveti) sadece 1. Viteste paraleldir. hiç bir durumda ise aynı değildir. Teker tabanında oluşan itme kuvveti lineerdir ve Newton cinsinden ifade edilir. Motor torku ise açısaldır ve NewtonMetre ile ifade edilir. Bu iki kuvvet arasında bir ilişki vardır. Teker tabanındaki kuvvetin kaynağı motor torkudur ama kendisi değildir. İkisi son kertede farklı şeylerdir. Bunu aşağıda örnekleriyle göreceğiz. Motor şaftını doğrudan tekere bağlasaydık bu iki kuvvet tümüyle paralel olacaktı, ne var ki araya torku ve RPMi istediğimiz gibi artırıp azaltan bir mekanizma, transmisyonu koyduğumuz için bu iki kuvvet arasındaki ilişki karmaşıklaşır. Yukarıdaki Newton formülüne ( A = F/M) motor torkunu yerleştiremezsiniz çünkü tork NM cinsindendir, oysa formüldeki F Newton cinsinden olmak zorundadır. Örnek vermek gerekirse 1200 kg ağırlığındaki bir aracın 1 Glik ivme ile hızlanabilmesi için kuvvet ne olmalıdır? F = MAdan 1200 x 9,81 = 11,772 Newton. Peki bu arabanın maksimum torku 1750 RPMde 240 NM olsun. Teker tabanında oluşan 11,772 Nluk kuvveti 240 NMlik motor torku ile nasıl ilişkilendireceğiz? Formüle doğrudan motor torkunu koyamadık çünkü birimler farklı. Gördüğünüz üzere A = F/M formülü motor torku için işlemiyor. Öyleyse motor torku ile tekerlek tabanındaki kuvveti nasıl ilişkilendireceğiz? Onu da BEYGİR GÜCÜ AKSELERASYON İLİŞKİSİ başlığı altında inceleyeceğiz.
BEYGİR GÜCÜ AKSELERASYON İLİŞKİSİ
Akselerasyonu açıklarken Newtonun ikinci yasasına atıfta bulunmuştuk. Yine bu yasaya göre, herhangi bir akselerasyondan söz edebilmemiz için kuvvet nesneye sıfırdan farklı bir zaman diliminde nesneyle AYNI HIZDA uygulanmalıdır. Açarsak, akselerasyonun şartı;
1. Kuvvet nesneye nesnenin sahip olduğu hızda uygulanacak, nesneyle aynı hızda uygulanacak,
2. Kuvvetin uygulama süresi 0dan farklı olacak.
Peki, güç tanımını hatırlayalım: belli bir hızda ve belli bir zaman zarfında uygulanan kuvvet. Bu tanım ile akselerasyonun şartları aynı. Demek ki, bir nesne üzerine uygulanan akslerasyon kuvveti o hızda uygulanan güç tarafından belirleniyor ! Bunu arabaya uygularsak aşağıdaki sonuçlara ulaşırız:
Akstaki Beygir Gücü = Dönüş Hızı x Tork
Lastik Tabanındaki Beygir Gücü = Kuvvet x Hız - buradan:
Akselerasyon Kuvveti (Fa) = Güç ( P) / Hız (V).
Yani Akselerasyon = Güç / Hız.
Nereden nereye geldik... Durmayalım, devam edelim:
Güç = Kuvvet x Hız ise (bu aynı zamanda beygi gücü tanımımızdır) ve Kuvvet = Kütle x Akselerasyon ise Güç = Kütle x Akselerasyon x Hız olur. Buradan:
Akselerasyon = Güç / Kütle x Hız denklemini elde ederiz. Momentum = Kütle x Hız olduğuna göre formülümüzü Akselerasyon = Güç / Momentum olarak sadeleştirebiliriz.
Newtonun ikinci yasası bizi A = F/Mden A = P / V ye, oradan da A = P / M e getirdi. Bu formülden görüleceği üzere akselerasyon ve hız ters orantılı. Hız arttıkça akselerasyon azalıyor, güç arttıkça akselerasyon artıyor.
Beygir gücünün akselerasyon ile ilişkisi açık. F = MA formülü uyarınca maksimum akselerasyon daima maksimum tork noktasında gelir ama bu tork motor torku değildir, tekerlek aksı torkudur. Tekerlek aksında tork maksimum olduğunda motorda tork maksimumda olmayabilir çünkü araya transmisyon girmiştir. İşte bu nedenle tekerlekteki maksimum kuvveti belirlerken motor torkuna değil, beygirgücüne bakacağız,..
Tüm bu açıklamalardan çıkan sonuç, akselerasyon söz konusu olduğunda belirleyici olan kuvvetin motor torku değil, tekerlek tabanında oluşan kuvvet olduğudur. Çünkü arabayı zemin üzerinde ileriye iten kuvvet budur, motor torku değil. Bu kuvvet transmisyon yüzünden motor torkundan farklıdır. Transmisyon motor torkuyla tekerlek taban kuvveti arasındaki doğrudan ilişkiyi kırar ve onu dolaylı hale getirir. Bunu aşağıdaki örneklerde göreceğiz. Sonuç olarak bizim için esas olan tekerlek taban kuvvetidir ve Tekerlek tabanındaki bu kuvvet iki yöntemle hesaplanabilir:
1. Tork yöntemi:
Tekerlek Taban Kuvveti (N) = (Tork (NM) x Şanzıman Oranı x Diferansiyel oranı) / Lastik yarıçapı (m)
2. Beygir Gücü Yöntemi:
Tekerlek Taban Kuvveti (N) = 820,275 x (Güç (HP) / Hız (Kms)
Hangi yöntemle hesaplarsanız hesaplayın, tekerlek taban kuvveti olarak aynı sonucu elde edersiniz.
Araya transmisyon girdiğinde motordaki tork tekerlek tabanına nasıl yansır bunu geçerli bir örnekle görelim:

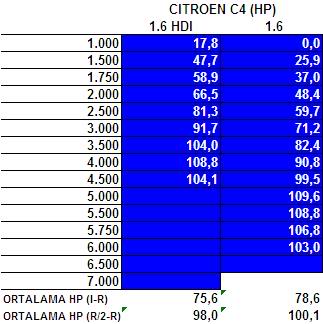
Tabloda verili değerler 2007 Citroen C4 1.6 hdI Picasso modeline aittir. Tablodan görüleceği üzere motor torku herhangi bir devirde sabit olduğu halde tekerlek tabanındaki kuvvet seçilen vitese bağlı olarak değişmektedir. Tablodaki örnekte 240 NM maksimum motor torku 1.750 RPMde geliyor. Motor 1.750 RPMdeyken 1. Vites ile 6. Vites arasında 9.333 Newtondan 2.004 Newtona kadar teker tabanındaki kuvvet değişiklik arz ediyor, oysa motorun torku değişmiyor, o maksimumda ama teker tabaındaki kuvvet seçilen vitese bağlı olarak sürekli değişiyor. Tekerlek tabanındaki kuvvetle motor torkunun örtüştüğü tek bir yer var: 1. vites. Aracın maksimum hızlanması 1. viteste gerçekten motorun maksimum torkuna paraleldir. Ne var ki , vites değiştirdiğinizde işin rengi değişiyor, 1. viteste varolan bu ilişki kırılıyor. Örneğin 2. viteste motor 1.750 RPMdeyken tekerlek tabanındaki kuvvet 5.062 N ve ikinci vites içindeki en yüksek taban kuvveti bu devirde geliyor. Ama aynı yol hızında vitesi 1e alırsak 8.400 Newtondan 6.400 Newtona azalan bir taban kuvveti elde ediyoruz. Diyelim ki 3. viteste maksimum tork devrinde (motor 1.750 RPMdeyken) seyahat ediyorsunuz. Bu durumda yol hızınız 45,5 kms, tekerlek devriniz 375 RPM olur. Şimdi hızlanmaya karar verdiniz. Bir de baktınız motor 1750 RPMde yani maksimum torkunu verdiği devirde. Şöyle düşünüyorsunuz: Madem ki A = F/M, o halde en yüksek hızlanmayı şimdi elde ederim . Yanlış!.. O esnada gaza basarsanız, elde edeceğiniz maksimum taban kuvveti 3.480N ama bir alt vitese yani ikinci vitese geçerseniz yol hızınıza eşit motor devri 2.543 RPM ve o RPMdeki motor torkunuz 232 NMnin altında ama 2. vites 375 RPMde tekerlek tabanındaki kuvvet tam 4.800 N (!)
Evet, aracın maksimum hızlanacağını düşündüğünüz anda teker tabanında 3.480 N kuvvet vardı ama bir alt vitese geçtiniz ve 3.480Ndan 4.800 Na çıktınız. Hani motor maksimum torkunu verdiği devirde aracımız da maksimum hızlanmaya sahip oluyordu?.. Yok öyle bir şey!
Konuyu bu noktadan irdelemeye devam edelim...
Aşağıda ağırlıkları ve diğer özellikleri birbirinin aynı 3 motora ait grafikler göreceksiniz. Bu üç motoru kırmızı, yeşil be mavi motor olarak adlandıralım. BU 3 motoru da birbirinin tıpatıp aynı 3 ayrı otomobile monte edelim ve neler oluyor bir göz atalım:

Yukarıdaki illüstrasyondan görüleceği üzere ilk motorumuz Mavi motor. 2000 RPMde 200 NM torka sahip ve 56 HP gücünde. 2:1 oranlı bir vites kutusuna bağlı. Bu vites kutusu da yine 2:1 oranlı bir diferansiyele bağlı. Diferansiyel aksları 195/65R15 ebatlarında bir tekerleği döndürüyor. Motorumuz 200 NM tork verdiği 2000 RPMde çalışırken vites kutusu bunu 2:1 oranla 1000 RPMe düşürüyor, vites kutusundan sonra gelen diferansiyel de devri 1.000 RPMden 500 RPMe düşürüyor. 500 RPMde dönen bir 195/65R15 tekerlek dakikada 997 metre yani saatte 59,8 km hızla yol alıyor. Özetle; 1.000 kg ağırlığındaki otomobilimiz Mavi motorla donatılmış ve saatte 59,8 km hızla yol alıyor. Bu hızdayken tekerlek tabaındaki kuvvet 2522 Newton. Yani aracımız Mavi motorla 2000 RPMdeyken 59,8 kms hızla yol alıyor. Bu hızda motorun torku 200 NM, beygir gücü 56 HP, lastik tabanındaki kuvvet ise 2.522 Newton. Şimdi de ikinci illüstrasyona bakalım:

Otomobilimiz aynı ama motorumuz bu defa Yeşil motor ve şu özelliklere sahip: 4.000 devirde 100 NM tork üretiyor. Bu devirde beygir gücü yine 56 HP. Diğer otomobilden tek farkı aynı yol hızında gidebilmek için 2:1 yerine 4:1 oranlı bir diferansiyele sahip. Bu sayede otomobilimiz yine aynı hızda, 59,8 kms ile yol alabiliyor. Peki bu durumda tekerlek tabanında oluşan kuvvet ne? Yine aynı, 2.522 Newton. Şimdi de 3. İllüstrasyona bakalım:

Kırmızı motorla donatılmış otomobilimiz de aynı hızla yol alıyor: 59,8 kms. Bu hıza ulaşmak için otomobilimiz yeşil motorlu otomobildekiyle aynı 4:1 oranlı diferansiyel kullanıyor çünkü Kırmızı motor 4000 RPMde 200 NM tork üretirken beygir gücü de diğer iki motorun iki katı yani 112 HP güce sahip. Peki bu otomobilin tekerlek tabaında oluşan kuvvet ne? Tam 5.044 Newton, diğer iki otomobilin 2 katı!. Şimdi senaryo şu:
Birbirinin aynı 3 otomobil var, ağırlıkları (1.000 kg) ve tekerlekleri aynı, sadece motorları farklı. Her biri bu 3 motorla donatılmış durumda ve yolda 59,8 kms hızla yan yana yol alıyorlar. Peki aynı anda dibine kadar gaza bassalar hangisi daha çabuk hızlanır?
1. 2.000 RPMde 200 NM tork üreten Mavi motorlu otomobil mi? (56 HP)
2. 4.000 RPMde 100 NM tork üreten Yeşil motorlu otomobil mi? (56 HP)
3. 4.000 RPMde 200 NM tork üreten Kırmızı motorlu otomobil mi? (112 HP)
Bunu anlamak için bakacağımız yer gördüğünüz gibi motorun torku değil çünkü Mavi motorla Kırmızı motorun torkları aynı. Peki nereye bakacağız? Elbette ki, tekerlek tabanında oluşan kuvvete:
1. Mavi motorlu otomobil: 2.522 N A = F / M = 2522/1000 = 2,522 m/s
2. Yeşil motorlu otomobil: 2.522 N A = F / M = 2522/1000 = 2,522 m/s
3. Kırmızı motorlu otomobil: 5.044 N A = F / M = 5044/1000 = 5,044 m/s
Demek ki, ~60 kms hızda giderken en yüksek akselerasyon değerine Kırmızı motorlu otomobil sahip olacak. Kırmızı otomobil aynı zamanda diğerleri arasında en yüksek beygir gücüne (56/56/112 HP) sahip olan otomobil!...
Bu sonuç hiç şaşırtıcı değil. Yukarıda bir yerlerde motor torkuyla tahrik tekerleri arasındaki ilişkiyi transmisyon kırıyor demiştik. Nasıl kırdığını işte gördünüz. Bu olguyu CVT şanzımanlı bir otomobilde daha iyi anlarız çünkü CVT şanzıman tork ve RPM arasındaki ilişkiyi her devirde bire bir tutturan bir şanzıman türüdür, en ideal şanzıman türüdür. Bir de CVT şanzımanlı bir araca bakalım:

Yukarıdaki tablodan görüleceği üzere CVT şanzımanda sabit bir hızda en yüksek hızlanma maksimum beygir gücünün oluştuğu noktada geliyor: 6.000 RPM 371 HP ve 4.875 N.
Ama sabit bir viteste, aynı vites içinde kalma kaydıyla ve hız sabit değilken en yüksek taban kuvveti maksimum torkun oluştuğu 4.200 RPMde 349 NMde geliyor: 5.235 N. BU durum gerçek hayatta sadece 1. vites hızlanmalarına tekebul ediyor, onun dışında her viteste sabit bir hızdayken maksimum hızlanma bir alt viteste genellikle maksimum beygir gücünün oluştuğu devirde veya o civarda geliyor.
Öyleyse ne zaman vites değiştireceğiz? Klasik CVT şanzımanlı bir araçta vites sürekli değiştiği için, maksimum teker kuvveti daima maksimum HP devrinde gelir, bunu yukarıda gördük. Ama bizim araçlarımız CVT şanzımanlı değil. Öyleyse ne zaman vites değiştirelim maksimum hızlanma için?
Elbette asla maksimum tork devrinde değil ama isterseniz bunu ayrı bir konu başlığı olarak ele alalım çünkü mevcut konu mini bir kitap yazacak kadar uzadı.
Onun yerine beygir gücü ile ilgili hesaplamalara devam edelim:
Şöyle bir senaryo oluşturalım: 200 LBF ( 272 Nm) torku 3.000 devirde (114 HP) ve 5.000 devirde (190 HP) üreten iki otomobil 0-160 parkurunda yarışırsa ne olur? Olacak olan şu: 1. otomobil yarışın hemen başında öne geçer, neden? Çünkü 2. otomobil daha az tork üretirken, ilk otomobil 200 LBF torku ondan önce 2.000 devirde üretir. Ama daha sonra 1. otomobilnın deviri arttıkça ürettiği tork azalacak, o vitesteki son hıza ulaşacak ve dişli oranları yüzünden daha az tork üreteceği (ve daha yavaş hızlanacağı) 2. vitese geçmek zorunda kalacak. Oysa 2. otomobil çok yüksek devirlere kadar 1. viteste kalabilir. Böylece 1. otomobil 3. vitese geçtiğinde 2. otomobil 2. vitese yeni geçmiş olacaktır ve sonuçta yarışı 2. otomobil kazanır. Burdan çıkan sonuç ne? Her iki otomobilin torkları aynı olduğu halde yarışı beygir gücü fazla olanın kazanacağıdır. Birinin beygir gücü fazladır çünkü aynı torka rağmen %66 daha fazla RPMe sahiptir. İşte bu fazla RPM ihtiyaç (hızlanma) anında torka çevrilir. Unutmayın, yüksek RPM ve yüksek tork yüksek beygir gücü demektir.
Şimdi de bir başka örnek: 1.000 kg ağırlığında bir otomobili 0 KMS hızdan (0 m/s) hızdan 100 KMS (27,78 m/s) hıza 10 saniyede çıkarmak ve aynı arabayı yine 10 saniyede 100 KMS hızdan hızdan 200 KMS (55,56 m/s) hıza çıkarmak ne kadar kuvvet gerektirir?
Her iki durumda da a=(27,78-0)/10=2,778 ve a=(55,56-27,78)/10=2,778. Yani ivme 2,778 m/s^2 (veya 0,35 G) )
f=m*a olduğuna göre f=1.000*2,778=2.778 N. Yani arabayı ister 0dan 100 km/s hıza, ister 100den 200 km/s hıza çıkartın, daima aynı miktarda KUVVETE yani torka ihtiyacınız var.
Ama 2.778 N kuvveti 0 m/s hızda ve 55,56 m/s aynı kuvveti kullanmak aynı sonucu doğurmuyor. İsterseniz gerekli gücü d = d1 + V1.t + (½).a.t^2 ve P= E/T formüllerini kullanarak bulalım:
x=0+0*10+0,5*2,778*10^2=138,9 m yani 0 m/s hızdan 27,78 m/s hıza 10 saniyede ulaşana kadar otomobilin katettiği mesafe. Peki diğeri ne? x=0+27,78*10+0,5*2,778*10^2=694,5 m bu da 27,78 m/s hızdan 55,56 m/s hıza ulaşana kadar katettiği mesafe.
İş formulü W = F x D olduğuna göre W=1.000*138,9=138.900 Jul ve P=138900/10=13.890 Watt (18,6 HP) W=1.000*694,5=694.500 Jul ve P=694.500/10=69.450 Watt (93,0 HP)
Sonuçta görüldüğü üzere iki otomobili de eşit miktarda hızlandırmak için aynı miktarda kuvvet yani tork gerekiyor ama daha hızlı olan arabayı hızlandırmak için tam 5 katı fazla beygir gücü gerekiyor. a = p/mv denklemine göre hızı ne kadar artırırsak, hızlanma o kadar azalıyor, Bu durumda gücü aynı oranda artırmak gerek hızlanmayı sabit tutmak için.
Özetlersek, vites değiştirmediğiniz zaman aynı viteste kalarak yapılan hızlanmada, aracınızın hızlanma grafiği, motorunuzun tork grafiğinin bir izdüşümüdür ve böyle bir hızlanmada aracınızın tork grafiğinin altında kalan alanın büyüklüğü bize hızlanmadaki başarımızı verir.
Ama ya vites değiştiriyorsak, ki değiştiriyoruz; o zaman ne olur? O zaman aracımızın hızlanma grafiği tork eğrisini değil HP eğrisini izler.
Yine bu topik veya bir başka topik altında beygir gücü grafiklerini nasıl okumalıyız meselesini de tartışmaya açmak istiyorum. Beygir gücü grafiklerini iyi okuyarak spesifik bir otomobille ilgili çok şey öğrenebiliriz. Bunun için güç bandı kavramını iyi anlamamız gerekiyor. Her motorun bir güç bandı vardır. Bu güç bandı temelde ikiye ayrılır:
1. Toplam Güç Bandı: rölanti devrinden, redline devirne kadar tüm devirleri kapsayan güç bandıdır.
2. Operasyonel Güç Bandı: Bırakın yarışları, günlük kullanımda dahi 1. vites haricinde hemen hiç kullanılmayan ilk 1500-2000 rpm dışarda bırakılarak hesaplanan güç bandı.
Bu iki güç bandına bakarak motorla ilgili şu değerleri elde edebiliriz:
a. Maksimum HPnin %80inin devir badının % kaçında yer aldığını görebilir ve diğer araçlarla kıyaslayabiliriz.
b. İster toplam güç bandı isterse operasyonel güç bandı içindeki ortalama HPyi hesaplarız. BU değer maksimum HPden daha önemlidir.
c. Güç bandını rölanti-redline arası belirleyebileceğimiz gibi, mesala redline/2 redline arası sınırlı tutabiliriz (eğer yarışıyorsak redline/2nin altı çok önemli değildir).

Yani beygir gücün grafiğini yukarıdaki örnekte olduğu gibi çeşitli yöntemlerle anlamlandırabiliriz. Dilerseniz bunu da bir başka topik altında ele alalım.
SONUÇ
Beygir gücü bize torkun hızını verir. Hızlı tork, yani yüksek devirde yüksek tork hedeftir, idealdir, Yüksek devirde yüksek tork, yüksek beygir gücü demektir. Düşük devirde yüksek tork ise düşük devirde yüksek beygir gücü demektir. Açalım...
1000 RPMde 200 LBF tork veren motor, 2000 RPMde 100 LBF tork veren motordan farksızdır. Çünkü ikisi de devri 1500 RPMe düşüren/çıkaran bir transmisyonla ( 1,5:1/0,75:1) eşitlenir. Tork her iki motor için 1500 RPMde eşitlenir: 133 LBF. Neden? Çünkü bu iki motor beygir gücü açısından eşittir: 38 HP. Dikkat ederseniz hem 1000, hem 1500 hem de 2000 RPMde HP aynıdır, değişmez çünkü bu iki motorun torkları farklıdır ama RPMleri onları hem kuvvet hem de HP açısından eşitler.
Tork yüksek devirde gelirse, yüksek HP elde ederiz. Yüksek devirde gelen tork bize daha fazla hız için kuvvetten ya da daha fazla kuvvet için hızdan fedakarlık yapma imkanı tanır ama düşük devirde gelen tork bize bu imkanı tanımaz. 10 RPMde 20.000 LBF veren bir motor devasa bir torka sahiptir ve 0-10 RPM arasında müthiş bir hızlanma sağlar ama aracımız bu müthiş hızlanma zarfında topu topu 20 metre yol alır çünkü bu devirdeki beygir gücü sadece 38 HPdir! HIZ OLMADAN HIZLANMA BİR HİÇTİR. Bize hızı veren şey ise RPMdir, tek başına tork değil. RPM ve tork birarada bize beygir gücünü verir. Bizim her halukarda bilmemiz gereken yegane şey beygir gücüdür, tork değil. 2000 RPMde 200 LBF tork veren bir motor 2000 RPMde 100 LBF tork veren bir motordan aynı devirde iki kat fazla beygir gücüne sahiptir (38 HPye karşı 76 HP) ama aynı motor 4000 RPMde 100 LBF tork veren motorla aynıdır çünkü 2:1lik bir transmisyon bu iki motoru hemen eşitler. Oysa beygir güçleri değişmez: 76 HP. Transmisyon dişli oranlarıyla artıp azaltılabildiği için torku bilmemize gerek yoktur, torku biliyorsak transmisyon dişli oranlarını da bilmemiz gerekir, aksi halde bildiğimiz tork değerleri bir işe yaramaz. Arabamız sadece motordan ibaret değildir, şanzımanı, diferansiyeli ve tekerlekleri de vardır, bunlar da hesaba katıldığında motor torkunun tekbaşına bir anlamı kalmaz. Oysa beygir güxünü biliyorsak ne şanzıman ne de diferansiyel dişli oranlarıyla uğraşmamıza gerek kalmaz. Zaten beygir gücü dediğimiz şey belirli bir torkun hangi devirde geldiğinden başka bir şey değildir.
Arabalar söz konusu olduğunda bilmemiz gereken tek büyüklük BEYGİR GÜCÜDÜR, torku unutun.
Ve evet, son olarak şu meşhur mottoya gelelim: HP araba sattırır, tork yarış kazandırır. Bu durum motor torku söz konusu olduğunda doğru değil, bunu gördük. Doğrusu ne?
Doğrusu şu:
Maksimum HP araba sattırır, ortalama HP yarış kazandırır.
SÖZÜN ÖZÜ:
TORK VE RPM TRANSMİSYON (MANİVELA) ARACILIĞI İLE BİRBİRLERİNE DÖNÜŞTÜRÜLEBİLEN FİZİKSEL BÜYÜKLÜKLERDİR. HIZ İÇİN RPME, HIZLANMA VE YÜK ÇEKME/TAŞIMA İÇİN TORKA İHTİYAÇ DUYARIZ. İHTİYAÇ DUYDUĞUMUZDA ELİMİZDEKİ FAZLA RPMİ TORKA, FAZLA TORKU DA RPME ÇEVİRİRİZ. ÖRNEĞİN RPMİ YARIYA DÜŞÜREREK TORKU İKİ KATINA YA DA TORKU YARIYA DÜŞÜREREK RPMİ İKİ KATINA ÇIKARIRIZ. BEYGİR GÜCÜ ELİMİZDEKİ RPMİN NE KADARINI TORKA YA DA ELİMİZDEKİ TORKUN NE KADARINI RPME ÇEVİREBİLECEĞİMİZİ GÖSTEREN HESAPLANABİLİR BİR NİCELİKTİR. DOLAYISIYLA İÇİNDE HEM TORKU HEM DE RPMİ BARINDIRIR. NE KADAR FAZLA BEYGİR GÜCÜMÜZ VARSA RPM/TORK DÖNÜŞÜMÜNDE O KADAR ÇOK ESNEKLİĞİE KAVUŞURUZ. BU NEDENLE MOTORUMUZLA İLGİLİ BİLMEMİZ GEREKEN TEK FİZİKSEL NİCELİK BEYGİR GÜCÜDÜR. BUNU BİLİYORSAK, DİĞERLERİNİ BİLMEYE GEREK YOKTUR.
ALINTIDIR